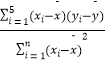题目内容
【题目】如图，在三棱锥A﹣BCD中，平面ABC⊥平面BCD，△BAC与BCD均为等于直角三角形，且∠BAC=∠BCD=90°，BC=2，点P是线段AB上的动点，若线段CD上存在点Q，使得异面直线PQ与AC成30°的角，则线段PA长的取值范围是（ ） 
A.（0， 
）
B.[0， 
]
C.（ ， 
）
D.（ ， ）
【答案】B
【解析】解：以C为原点，CD为x轴，CB为y轴，过C作平面BCD的垂线为z轴， 建立空间直角坐标系，
则A（0，1，1），B（0，2，0），C（0，0，0），
设Q（q，0，0）， 
=（0，λ，﹣λ），
则 
= 
﹣ 
= 
=（q，0，0）﹣（0，1，1）﹣（0，λ，﹣λ）=（q，﹣1﹣λ，λ﹣1），
∵异面直线PQ与AC成30°的角，
∴cos30°= 
= 
= 
= 
，
∴q2+2λ2+2= 
，∴ 
，
∴ 
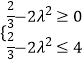，解得0 
，
∴| 
|= 
∈[0， 
]，
∴线段PA长的取值范围是[0， ]．
故选：B．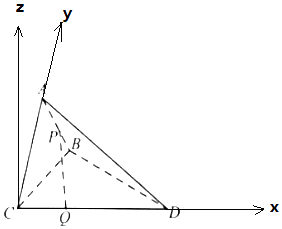
练习册系列答案
相关题目
