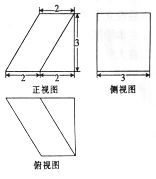
题目内容
【题目】设函数![]() ,其中
,其中![]() 是函数
是函数![]() 的导数.
的导数.
(1)求![]() 的单调区间;
的单调区间;
(2)对于![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(1)![]() 的递减区间为
的递减区间为![]() ,递增区间为
,递增区间为![]() ;(2)
;(2)![]() .
.
【解析】【试题分析】(1)依据题设条件,先对函数求导,再运用导数与函数的单调性之间的关系分析求解;(2)借助题设条件,运用等价转化的思想及分类整合思想建立函数关系,借助导数知识分析求解:
(1)对![]() 求导,得
求导,得![]() .
.
令![]() ,得
,得![]() ,即
,即![]() ,于是
,于是![]() .
.
令![]() ,得
,得![]() ,即
,即![]() ,于是
,于是![]() .
.
由![]() ,得
,得![]() .
.
令![]() ,显然
,显然![]() 是其一根.
是其一根.
又因为![]() 递增,所以
递增,所以![]() 只有唯一根
只有唯一根![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 递减;当
递减;当![]() 时,
时,![]() ,则
,则![]() 递增.
递增.
所以![]() 的递减区间为
的递减区间为![]() ,递增区间为
,递增区间为![]() .
.
(2)不等式![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
令![]() ,则只需
,则只需![]() .
.
由![]() ,得
,得![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ,则
,则![]() 在
在![]() 车上递增,没有最小值,舍去;
车上递增,没有最小值,舍去;
②当![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 递减;
递减;
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 递增.
递增.
所以![]() .
.
于是只需![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
令![]()
![]() ,由
,由![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 递增;
递增;
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 递减.
递减.
所以![]() ,于是
,于是![]() ,即
,即![]() 的最大值为
的最大值为![]()

 名校课堂系列答案
名校课堂系列答案【题目】某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
年份200 | 0 | 1 | 2 | 3 | 4 |
人口数 | 5 | 7 | 8 | 11 | 19 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)据此估计2005年该城市人口总数.
参考公式: 用最小二乘法求线性回归方程系数公式 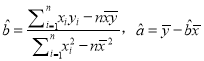
【题目】(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
甲 | 82 | 82 | 79 | 95 | 87 |
乙 | 95 | 75 | 80 | 90 | 85 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
【题目】宁夏某市2008年至2012年新建商品住宅每平方米的均价![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 |
年份序号x | 1 | 2 | 3 | 4 | 5 |
每平米均价y | 2.0 | 3.1 | 4.5 | 6.5 | 7.9 |
(Ⅰ)求y关于x的线性回归方程![]() ;
;
(Ⅱ)利用(Ⅰ)中的回归方程,分析从2008年到2012年该市新建商品住宅每平方米均价的变化情况,并预测该市2015年新建商品住宅每平方米的均价.
附:回归直线的斜率和截距的最小二乘估计公式分别为
 ,
, ![]()
【题目】某种多面体玩具共有12个面,在其十二个面上分别标有数字1,2,3,…,12.若该玩具质地均匀,则抛掷该玩具后,任何一个数字所在的面朝上的概率均相等.
为检验某批玩具是否合格,制定检验标准为:多次抛掷该玩具,并记录朝上的面上标记的数字,若各数字出现的频率的极差不超过0.05.则认为该玩具合格.

(1)对某批玩具中随机抽取20件进行检验,将每个玩具各面数字出现频率的极差绘制成茎叶图(如图所示),试估计这批玩具的合格率;
(2)现有该种类玩具一个,将其抛掷100次,并记录朝上的一面标记的数字,得到如下数据:
朝上面的数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
次数 | 9 | 7 | 8 | 6 | 10 | 9 | 9 | 8 | 10 | 9 | 7 | 8 |
1)试判定该玩具是否合格;
2)将该玩具抛掷一次,记事件![]() :向上的面标记数字是完全平方数(能写成整数的平方形式的数,如
:向上的面标记数字是完全平方数(能写成整数的平方形式的数,如![]() ,9为完全平方数);事件
,9为完全平方数);事件![]() :向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中
:向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中![]() 表示
表示![]() 的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件
的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件![]() 与事件
与事件![]() 有关.
有关.
|
| 合计 | |
| |||
| |||
合计 | 100 |
(参考公式及数据:![]() ,
,![]() )
)