题目内容
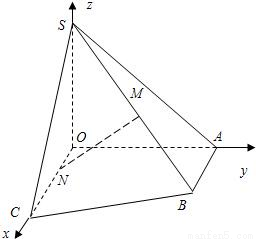
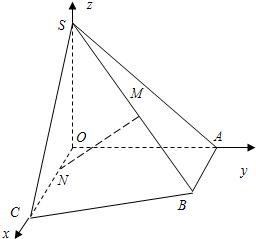 如图所示在直角梯形OABC中,∠COA=∠OAB=
如图所示在直角梯形OABC中,∠COA=∠OAB=| π | 2 |
点M是棱SB的中点,N是OC上的点,且ON:NC=1:3,以OC,OA,OS所在直线
建立空间直角坐标系O-xyz.
(1)求异面直线MN与BC所成角的余弦值;
(II)求MN与面SAB所成的角的正弦值.
分析:(1)先以O为原点,建立如图所示的空间直角坐标系,再求得相关点的坐标,再求的相关向量的坐标,最后用向量夹角公式求解.
(2)欲求MN与面SAB所成的角的正弦值,先利用待定系数法求出平面SAB的一个法向量,最后用向量夹角公式求解即可.
(2)欲求MN与面SAB所成的角的正弦值,先利用待定系数法求出平面SAB的一个法向量,最后用向量夹角公式求解即可.
解答: 解:如图建系,则S(0,0,1)C(4,0,0)A(0,1,0)B(1,1,0)
解:如图建系,则S(0,0,1)C(4,0,0)A(0,1,0)B(1,1,0)
所以N(1,0,0)M(
,
,
)(2分)
(1)
=(
,-
,-
)
=(-3,1,0)cos<
,
>=
=
=-
(5分)
∴直线MN与BC所成角的余弦值为
(6分)
(2)设平面SAB的一个法向量为
=(a,b,c)
则
•
=(a,b,c)•(1,1,-1)=a+b-c=0
•
=(a,b,c)•(0,1,-1)=b-c=0
令b=1可得法向量
=(0,1,1)(8分)
cos<
,
>=
=
=-
(9分)
∴直线MN与面SAB所成角的正弦值为
(10分)
 解:如图建系,则S(0,0,1)C(4,0,0)A(0,1,0)B(1,1,0)
解:如图建系,则S(0,0,1)C(4,0,0)A(0,1,0)B(1,1,0)所以N(1,0,0)M(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| CB |
| MN |
| CB |
| ||||
|
|
| -2 | ||||||
|
| 2 |
| 15 |
| 30 |
∴直线MN与BC所成角的余弦值为
| 2 |
| 15 |
| 30 |
(2)设平面SAB的一个法向量为
| n |
则
| n |
| SB |
| n |
| SA |
令b=1可得法向量
| n |
cos<
| MN |
| n |
| ||||
|
|
| -1 | ||||||
|
| ||
| 3 |
∴直线MN与面SAB所成角的正弦值为
| ||
| 3 |
点评:本题主要考查用向量法研究直线与平面所成的角和异面直线所成的角,选用向量法,避开了作辅助线,优越性很强,作为理科要注意应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•永州一模)如图所示,直角梯形ABCD中,∠A=∠D=90°,AD=2,AB=3,CD=4,P在线段AB上,BP=1,O在CD上,且OP∥AD,将图甲沿OP折叠使得平面OCBP⊥底面ADOP,得到一个多面体(如图乙),M、N分别是AC、OP的中点.
(2013•永州一模)如图所示,直角梯形ABCD中,∠A=∠D=90°,AD=2,AB=3,CD=4,P在线段AB上,BP=1,O在CD上,且OP∥AD,将图甲沿OP折叠使得平面OCBP⊥底面ADOP,得到一个多面体(如图乙),M、N分别是AC、OP的中点. ,OA=OS=AB=1,OC=4,
,OA=OS=AB=1,OC=4,
 ,OA=OS=AB=1,OC=4,
,OA=OS=AB=1,OC=4,
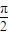 ,OA=OS=AB=1,OC=4,
,OA=OS=AB=1,OC=4,