题目内容
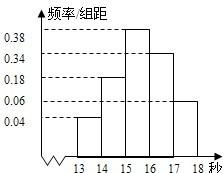 某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18]如图是按上述分组方法得到的频率分布直方图.
某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18]如图是按上述分组方法得到的频率分布直方图.(1)若成绩大于等于14秒且小于16秒规定为良好,求该班在这次百米测试中成绩为良好的人数.
(2)设m,n表示该班两个学生的百米测试成绩,已知m,n∈[13,14)∪[17,18]求事件“|m-n|>2”的概率.
分析:(Ⅰ)根据直方图矩形的面积表示频率,可知成绩在[14,16)内的人数;
(Ⅱ)成绩在[13,14)的人数有2人,设为a,b.成绩在[17,18]的人数有3人,设为A,B,C;基本事件总数为10,事件“|m-n|>2”由6个基本事件组成.根据古典概型公式可求出所求.
(Ⅱ)成绩在[13,14)的人数有2人,设为a,b.成绩在[17,18]的人数有3人,设为A,B,C;基本事件总数为10,事件“|m-n|>2”由6个基本事件组成.根据古典概型公式可求出所求.
解答:解:(Ⅰ)根据直方图可知成绩在[14,16)内的人数为:50×0.18+50×0.38=28人;(5分)
(Ⅱ)成绩在[13,14)的人数有:50×0.04=2人,设为a,b.
成绩在[17,18]的人数有:50×0.06=3人,
设为A,B,C.m,n∈[13,14)时有ab一种情况.
m,n∈[17,18]时有AB,AC,BC三种情况.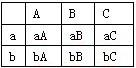
m,n分别在[13,14)和[17,18]时有aA,aB,aC,bA,bB,bC六种情况.
基本事件总数为10,事件“|m-n|>2”由6个基本事件组成.
所以P(|m-n|>2)=
=
(13分)
(Ⅱ)成绩在[13,14)的人数有:50×0.04=2人,设为a,b.
成绩在[17,18]的人数有:50×0.06=3人,
设为A,B,C.m,n∈[13,14)时有ab一种情况.
m,n∈[17,18]时有AB,AC,BC三种情况.

m,n分别在[13,14)和[17,18]时有aA,aB,aC,bA,bB,bC六种情况.
基本事件总数为10,事件“|m-n|>2”由6个基本事件组成.
所以P(|m-n|>2)=
| 6 |
| 10 |
| 3 |
| 5 |
点评:本题主要考查了频率分布直方图,以及古典概型的概率问题、用样本的数字特征估计总体的数字特征等有关知识,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
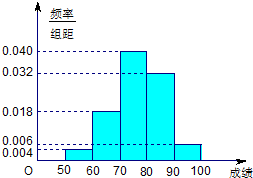 某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.
某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.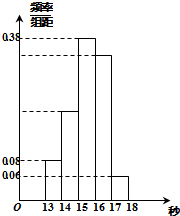 某班50名学生在一次百米测试中,成绩全部在[13,18]内,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15);…第五组[17,18].右图是按上述分组方法得到的频率分布直方图.且第一组,第二组,第四组的频数成等比数列,m,n表示该班某两位同学的百米测试成绩,且m,n∈[13,14)∪[17,18].则事件“|m-n|>1”的概率为( )
某班50名学生在一次百米测试中,成绩全部在[13,18]内,将测试结果按如下方式分成五组:第一组[13,14);第二组[14,15);…第五组[17,18].右图是按上述分组方法得到的频率分布直方图.且第一组,第二组,第四组的频数成等比数列,m,n表示该班某两位同学的百米测试成绩,且m,n∈[13,14)∪[17,18].则事件“|m-n|>1”的概率为( )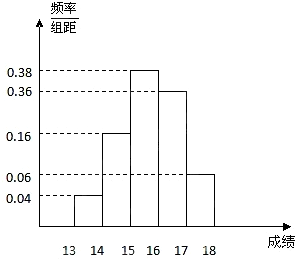 某班50名学生在一次百米测试中,成绩介于13秒与18秒之间.将测试结果分成五组,按上述分组方法得到如下频率分布直方图
某班50名学生在一次百米测试中,成绩介于13秒与18秒之间.将测试结果分成五组,按上述分组方法得到如下频率分布直方图
 某班 50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( )
某班 50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( )