题目内容
14.设数列{an}的前n项和为Sn,且满足a1=2,an+1=2Sn+2.(1)求a2;
(2)数列{an}的通项公式;
(3)设bn=$\frac{{a}_{n+1}}{{S}_{n+1}{S}_{n}}$,求数列{bn}的前n项和Tn.
分析 (1)令n=1代入计算即可得到;
(2)由数列的通项和求和的关系,结合等比数列的通项公式,即可得到所求;
(3)bn=$\frac{{a}_{n+1}}{{S}_{n+1}{S}_{n}}$=$\frac{2•{3}^{n}}{({3}^{n}-1)({3}^{n+1}-1)}$=$\frac{1}{{3}^{n}-1}$-$\frac{1}{{3}^{n+1}-1}$,再由裂项相消求和,化简即可得到.
解答 解:(1)a1=2,an+1=2Sn+2,
可得a2=2S1+2=2×2+2=6;
(2)an+1=2Sn+2,
当n≥2时,an=2Sn-1+2,
可得an+1-an=2(Sn-Sn-1)=2an,
即为an+1=3an,
则an=a2•3n-2=2•3n-1,
对n=1成立,
故数列{an}的通项公式为an=2•3n-1;
(3)bn=$\frac{{a}_{n+1}}{{S}_{n+1}{S}_{n}}$=$\frac{2•{3}^{n}}{({3}^{n}-1)({3}^{n+1}-1)}$
=$\frac{1}{{3}^{n}-1}$-$\frac{1}{{3}^{n+1}-1}$,
则数列{bn}的前n项和Tn=$\frac{1}{3-1}$-$\frac{1}{9-1}$+$\frac{1}{9-1}$-$\frac{1}{27-1}$+…+$\frac{1}{{3}^{n}-1}$-$\frac{1}{{3}^{n+1}-1}$
=$\frac{1}{2}$-$\frac{1}{{3}^{n+1}-1}$.
点评 本题考查数列的通项和求和之间的关系,考查等比数列的通项公式的运用,考查数列的求和方法:裂项相消求和,考查运算能力,属于中档题.

练习册系列答案
相关题目
6.已知集合A到B的映射f:(xy)→(x+y,xy),那么集合A中元素(4,3)在B中所对应的元素是( )
| A. | (1,3) | B. | (3,1) | C. | (7,12) | D. | (12,7) |
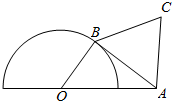 如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.
如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.