题目内容
 将杨辉三角中的每一个数Cnr都换成
将杨辉三角中的每一个数Cnr都换成| 1 | ||
(n+1)
|
| 1 | ||
(n+1)
|
| 1 | ||
(n+1)
|
| 1 | ||
n
|
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 30 |
| 1 |
| 60 |
| 1 | ||
n
|
| 1 | ||
(n+1)
|
| lim |
| n→∞ |
分析:通过观察可得
=
=
(
-
)=〔(1+
+
+…+
)-(
+
+…+
)〕+〔(
+
+
+
+…+
)-(
+
+…+
)〕=1-
+
-
=
+
-
.进而可得
an.
| 1 | ||
(n+1)•
|
| 2 |
| n•(n+1)•(n-1) |
| 1 |
| n |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n |
| lim |
| n→∞ |
解答:解:第一个空通过观察可得.
=
=
(
-
)
=
×
-
×
=
-
-
+
=
+
-
an=
+
+
+
++
+
=(1+
-1)+(
+
-
)+(
+
-
)+(
+
-
)+…+(
+
-
)+(
+
-
)
=(1+
+
+…+
)+(
+
+
+
+…+
)-2(
+
+…+
)
=〔(1+
+
+…+
)-(
+
+…+
)〕+〔(
+
+
+
+…+
)
-(
+
+…+
)〕
=1-
+
-
=
+
-
所以
an=
.
答案:
.
| 1 | ||
(n+1)•
|
| 2 |
| n•(n+1)•(n-1) |
| 1 |
| n |
| 1 |
| n-1 |
| 1 |
| n+1 |
=
| 1 |
| n |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 2 |
| n |
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 30 |
| 1 |
| 60 |
| 1 | ||
n
|
| 1 | ||
(n+1)
|
=(1+
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 2 |
| 4 |
| 1 |
| 4 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| n-2 |
| 1 |
| n |
| 1 |
| n-1 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 2 |
| n |
=(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
=〔(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| n+1 |
-(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
=1-
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n |
所以
| lim |
| n→∞ |
| 1 |
| 2 |
答案:
| 1 |
| 2 |
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目

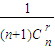 ,就得到一个如下图所示的分数三角形,成为莱布尼茨三角形,从莱布尼茨三角形可看出
,就得到一个如下图所示的分数三角形,成为莱布尼茨三角形,从莱布尼茨三角形可看出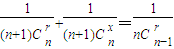 ,其中x=r+1,令
,其中x=r+1,令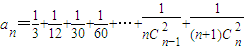 ,则
,则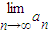 =
= 