题目内容
(2009山东卷理) (本小题满分14分)
设椭圆E: ![]() (a,b>0)过M(2,
(a,b>0)过M(2,![]() ) ,N (
) ,N (![]() ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且![]() ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
![]() ,
,![]()
解析:
解:(1)因为椭圆E: ![]() (a,b>0)过M(2,
(a,b>0)过M(2,![]() ) ,N (
) ,N (![]() ,1)两点,
,1)两点,
所以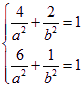 解得
解得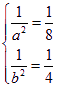 所以
所以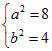 椭圆E的方程为
椭圆E的方程为![]()
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且![]() ,设该圆的切线方程为
,设该圆的切线方程为![]() 解方程组
解方程组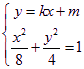 得
得![]() ,即
,即![]() ,
, ![]()
![]()
则△=![]() ,即
,即![]()
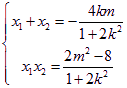 ,
,![]() 要使
要使![]() ,需使
,需使![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() 又
又![]() ,所以
,所以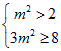 ,所以
,所以![]() ,即
,即![]() 或
或![]() ,因为直线
,因为直线![]() 为圆心在原点的圆的一条切线,所以圆的半径为
为圆心在原点的圆的一条切线,所以圆的半径为![]() ,
,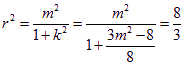 ,
,![]() ,所求的圆为
,所求的圆为![]() ,此时圆的切线
,此时圆的切线![]() 都满足
都满足![]() 或
或![]() ,而当切线的斜率不存在时切线为
,而当切线的斜率不存在时切线为![]() 与椭圆
与椭圆![]() 的两个交点为
的两个交点为![]() 或
或![]() 满足
满足![]() ,综上, 存在圆心在原点的圆
,综上, 存在圆心在原点的圆![]() ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且![]() .
.
因为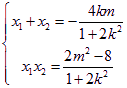 ,
,
所以![]() ,
,
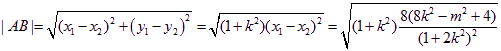
![]() ,
,
①当![]() 时
时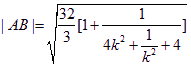
因为![]() 所以
所以 ,
,
所以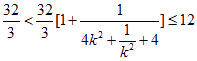 ,
,
所以![]() 当且仅当
当且仅当![]() 时取”=”.
时取”=”. ![]()
![]()
② 当![]() 时,
时,![]() .
.
③ 当AB的斜率不存在时, 两个交点为![]() 或
或![]() ,
,
所以此时![]() ,
,
综上, |AB |的取值范围为![]() 即:
即: ![]()

(2009山东卷理)(本小题满分12分)
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q![]() 为0.25,在B处的命中率为q
为0.25,在B处的命中率为q![]() ,该同学选择先在A处投一球,以后都在B处投,用
,该同学选择先在A处投一球,以后都在B处投,用![]() 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
| 0 | 2 | 3 | 4 | 5 |
| 0.03 | P1 | P2 | P3 | P4 |
(1) 求q![]() 的值;
的值; ![]()
![]()
(2) 求随机变量![]() 的数学期望E
的数学期望E![]() ;
;
(3) 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。