题目内容
(1)在(1+x)n的展开式中,若第3项与第6项系数相等,则n等于多少?(2)(x
| x |
| 1 | |||
|
(3)已知(x2-
| 1 |
| x |
| 1 |
| x |
分析:(1)利用二项展开式的通项公式求出第3项与第6项系数,列出方程解得.
(2)利用已知求出n,据二项展开式中间项的二项式系数最大,求出展开式中二项式系数最大的项.
(3)利用展开式的二项式系数和为2n,列出方程求出n,利用二项展开式的通项公式求出通项,据通项求出展开式中的系数最大的项和系数最小的项.
(2)利用已知求出n,据二项展开式中间项的二项式系数最大,求出展开式中二项式系数最大的项.
(3)利用展开式的二项式系数和为2n,列出方程求出n,利用二项展开式的通项公式求出通项,据通项求出展开式中的系数最大的项和系数最小的项.
解答:解:(1)由已知得Cn2=Cn5?n=7
(2)由已知得Cn1+Cn3+Cn5+=128,2n-1=128,n=8,
而展开式中二项式系数最大项是T4+1=
(x
)4(
)4=70x4
.
(3)解:2n-27=128,n=8,(x2-
)8的通项Tr+1=
(x2)8-r(-
)r=(-1)r
x16-3r
当r=4时,展开式中的系数最大,即T5=70x4为展开式中的系数最大的项;
当r=3,或5时,展开式中的系数最小,即T3-56x7,T6=-56x为展开式中的系数最小的项.
(2)由已知得Cn1+Cn3+Cn5+=128,2n-1=128,n=8,
而展开式中二项式系数最大项是T4+1=
| C | 4 8 |
| x |
| 1 | |||
|
| 3 | x2 |
(3)解:2n-27=128,n=8,(x2-
| 1 |
| x |
| C | r 8 |
| 1 |
| x |
| C | r 8 |
当r=4时,展开式中的系数最大,即T5=70x4为展开式中的系数最大的项;
当r=3,或5时,展开式中的系数最小,即T3-56x7,T6=-56x为展开式中的系数最小的项.
点评:本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工具;考查二项式系数的性质:展开式的中间项的二项式系数最大及展开式的二项式系数和为2n.

练习册系列答案
相关题目
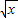 +
+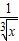 )n的展开式奇数项的二项式系数之和为128,则求展开式中二项式系数最大项.
)n的展开式奇数项的二项式系数之和为128,则求展开式中二项式系数最大项.