题目内容
(1)在(1+x)n的展开式中,若第3项与第6项系数相等,且n等于多少?(2)(x
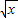 +
+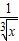 )n的展开式奇数项的二项式系数之和为128,则求展开式中二项式系数最大项.
)n的展开式奇数项的二项式系数之和为128,则求展开式中二项式系数最大项.
【答案】分析:(1)利用二项展开式的通项求出展开式的第3项与第6项系数,列出方程解出n.
(2)利用展开式的二项式系数性质列出方程求出n,利用二项展开式的二项式系数的性质中间项的二项式系数最大,
再利用二项展开式的通项公式求出展开式中二项式系数最大项.
解答:解:(1)由已知得Cn2=Cn5⇒n=7
(2)由已知得Cn1+Cn3+Cn5+…=128,
∴2n-1=128
∴n=8,
而展开式中二项式
系数最大项是 =70
=70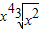 .
.
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题;本题考查二项式系数的性质.
(2)利用展开式的二项式系数性质列出方程求出n,利用二项展开式的二项式系数的性质中间项的二项式系数最大,
再利用二项展开式的通项公式求出展开式中二项式系数最大项.
解答:解:(1)由已知得Cn2=Cn5⇒n=7
(2)由已知得Cn1+Cn3+Cn5+…=128,
∴2n-1=128
∴n=8,
而展开式中二项式
系数最大项是
 =70
=70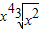 .
.点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题;本题考查二项式系数的性质.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目