题目内容
已知平面内一动点 P到定点 的距离等于它到定直线
的距离等于它到定直线 的距离,又已知点 O(0,0),M(0,1).
的距离,又已知点 O(0,0),M(0,1).(1)求动点 P的轨迹C的方程;
(2)当点 P(x,y)(x≠0)在(1)中的轨迹C上运动时,以 M P为直径作圆,求该圆截直线
 所得的弦长;
所得的弦长;(3)当点 P(x,y)(x≠0)在(1)中的轨迹C上运动时,过点 P作x轴的垂线交x轴于点 A,过点 P作(1)中的轨迹C的切线l交x轴于点 B,问:是否总有 P B平分∠A PF?如果有,请给予证明;如果没有,请举出反例.
【答案】分析:(1)根据抛物线的定义判定出动点 P是以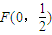 为焦点以
为焦点以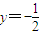 为准线的抛物线,直接写出其方程为x2=2y
为准线的抛物线,直接写出其方程为x2=2y
(2)根据圆的标准方程求出圆的方程,根据直线截圆的弦长公式弦长l=2 求出该圆截直线
求出该圆截直线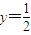 所得的弦长
所得的弦长
(3)根据导数的几何意义求出切线的斜率,利用直线的点斜式求出切线l的方程为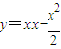 ,利用点到直线的距离公式求出B到PA的距离为
,利用点到直线的距离公式求出B到PA的距离为 ,再求出点B到直线PF的距离
,再求出点B到直线PF的距离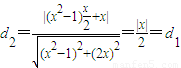 ,根据角平分线的判定得到总有PB平分∠APF.
,根据角平分线的判定得到总有PB平分∠APF.
解答:解:(1)根据题意,动点 P是以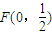 为焦点以
为焦点以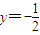 为准线的抛物线,
为准线的抛物线,
所以p=1开口向上,
所以动点 P的轨迹C的方程为x2=2y
(2)以 M P为直径的圆的圆心(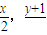 ),|MP|=
),|MP|=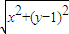 =
=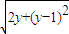 =
=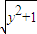
所以圆的半径r=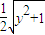 ,圆心到直线
,圆心到直线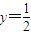 的距离d=|
的距离d=|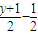 |=
|=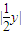 ,
,
故截得的弦长l=2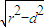 =
=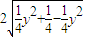 =1
=1
(3)总有 P B平分∠A PF.
证明:因为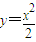
所以,y′=x,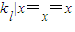 .
.
所以切线l的方程为 ,
,
令y=0得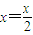 ,
,
所以B(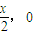 )
)
所以B到PA的距离为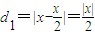
下面求直线PF的方程,
因为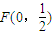
所以直线PF的方程为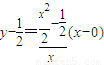 整理得
整理得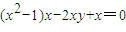
所以点B到直线PF的距离
所以 PB平分∠APF.
点评:本题考查导数的几何意义;直线与圆相交的弦长公式;点到直线的距离公式以及角平分线的判定,属于一道综合题.
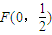 为焦点以
为焦点以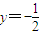 为准线的抛物线,直接写出其方程为x2=2y
为准线的抛物线,直接写出其方程为x2=2y(2)根据圆的标准方程求出圆的方程,根据直线截圆的弦长公式弦长l=2
 求出该圆截直线
求出该圆截直线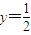 所得的弦长
所得的弦长(3)根据导数的几何意义求出切线的斜率,利用直线的点斜式求出切线l的方程为
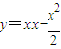 ,利用点到直线的距离公式求出B到PA的距离为
,利用点到直线的距离公式求出B到PA的距离为 ,再求出点B到直线PF的距离
,再求出点B到直线PF的距离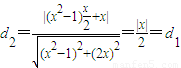 ,根据角平分线的判定得到总有PB平分∠APF.
,根据角平分线的判定得到总有PB平分∠APF.解答:解:(1)根据题意,动点 P是以
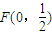 为焦点以
为焦点以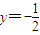 为准线的抛物线,
为准线的抛物线,所以p=1开口向上,
所以动点 P的轨迹C的方程为x2=2y
(2)以 M P为直径的圆的圆心(
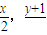 ),|MP|=
),|MP|=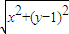 =
=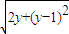 =
=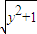
所以圆的半径r=
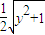 ,圆心到直线
,圆心到直线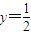 的距离d=|
的距离d=|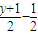 |=
|=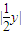 ,
,故截得的弦长l=2
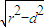 =
=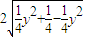 =1
=1(3)总有 P B平分∠A PF.
证明:因为
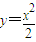
所以,y′=x,
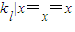 .
.所以切线l的方程为
 ,
,令y=0得
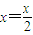 ,
,所以B(
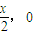 )
)所以B到PA的距离为
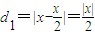
下面求直线PF的方程,
因为
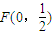
所以直线PF的方程为
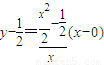 整理得
整理得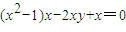
所以点B到直线PF的距离

所以 PB平分∠APF.
点评:本题考查导数的几何意义;直线与圆相交的弦长公式;点到直线的距离公式以及角平分线的判定,属于一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目