题目内容
某校从4名男教师和2名女教师中任选3人参加全县教育系统举行的“我的教育故事”演讲比赛.如果设随机变量ξ表示所选3人中女教师的人数.
求:
(1)ξ的分布列;
(2)ξ的数学期望;
(3)“所选3人中女教师的人数ξ≥1”的概率.
求:
(1)ξ的分布列;
(2)ξ的数学期望;
(3)“所选3人中女教师的人数ξ≥1”的概率.
分析:(1)(2)本题是一个超几何分步,随机变量ξ表示所选3人中女教师的人数,ξ可能取的值为0,1,2,结合变量对应的事件和超几何分布的概率公式,写出变量的分布列和数学期望.
(3)可以先求所选3人中女教师人数ξ≤1,表示女教师有1个人,或者没有女生,根据第一问做出的概率值,根据互斥事件的概率公式得到结果.
(3)可以先求所选3人中女教师人数ξ≤1,表示女教师有1个人,或者没有女生,根据第一问做出的概率值,根据互斥事件的概率公式得到结果.
解答:解:(1)由题意知本题是一个超几何分步,
随机变量ξ表示所选3人中女教师的人数,ξ可能取的值为0,1,2.
P(ξ=k)=
,k=0,1,2
∴ξ的分布列为:
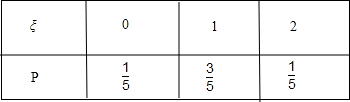
(2)∴ξ的数学期望为Eξ=0×
+1×
+2×
=1,
(3)由(1)知“所选3人中女生人数ξ≥1”的概率为P(ξ≥1)=P(ξ=1)+P(ξ=2)=
+
=
,
∴所选3人中女教师的人数ξ≥1为:
;
随机变量ξ表示所选3人中女教师的人数,ξ可能取的值为0,1,2.
P(ξ=k)=
| ||||
|
∴ξ的分布列为:

(2)∴ξ的数学期望为Eξ=0×
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
(3)由(1)知“所选3人中女生人数ξ≥1”的概率为P(ξ≥1)=P(ξ=1)+P(ξ=2)=
| 3 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
∴所选3人中女教师的人数ξ≥1为:
| 4 |
| 5 |
点评:本小题考查离散型随机变量分布列和数学期望,考查超几何分步,考查互斥事件的概率,考查运用概率知识解决实际问题的能力.

练习册系列答案
相关题目