题目内容
已知tan2θ=-2| 2 |
| π |
| 2 |
| cosθ-sinθ | ||||
|
分析:通过正切的倍角公式根据tan2θ求出tanθ的值;先用正弦两角和公式对原式进行化简,再tanθ代入即可得到答案.
解答:解:tan2θ=
=-2
,即
tan2θ-tanθ-
=0又∵
<θ<
∴tanθ=
=
=
=
=
=2
-3
| 2tanθ |
| 1-tan2θ |
| 2 |
| 2 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 2 |
| cosθ-sinθ | ||||
|
| cosθ-sinθ | ||||||||||
|
| cosθ-sinθ |
| cosθ+sinθ |
| 1-tanθ |
| 1+tanθ |
1-
| ||
1+
|
| 2 |
点评:本题主要考查三角函数中的两角和公式运用,在求tanθ的过程中,要注意定义域,属基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
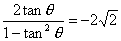 的值.
的值. ,π<2θ<2π,则tanθ的值为
,π<2θ<2π,则tanθ的值为
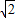 ,π<2θ<2π,则tanθ的值为( )
,π<2θ<2π,则tanθ的值为( )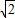
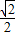
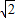 或-
或-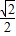
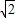 ,π<2θ<2π.
,π<2θ<2π.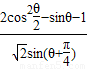 的值.
的值.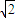 ,π<2θ<2π.
,π<2θ<2π.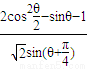 的值.
的值.