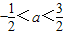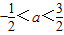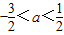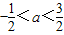题目内容
定义算式?:x?y=x(1-y),若不等式(x-a)?(x+a)<1对任意x都成立,则实数a的取值范围是( )
分析:由已知中算式?:x?y=x(1-y),我们可得不等式(x-a)?(x+a)<1对任意x都成立,转化为一个关于x的二次不等式恒成立,进而根据二次不等式恒成立的充要条件,构造一个关于a的不等式,解不等式求出实数a的取值范围.
解答:解:∵x?y=x(1-y),
∴若不等式(x-a)?(x+a)<1对任意x都成立,
则(x-a)•(1-x-a)-1<0恒成立
即-x2+x+a2-a-1<0恒成立
则△=1+4(a2-a-1)=4a2-4a-3<0恒成立
解得-
<a<
故选D
∴若不等式(x-a)?(x+a)<1对任意x都成立,
则(x-a)•(1-x-a)-1<0恒成立
即-x2+x+a2-a-1<0恒成立
则△=1+4(a2-a-1)=4a2-4a-3<0恒成立
解得-
| 1 |
| 2 |
| 3 |
| 2 |
故选D
点评:本题考查的知识点是二次函数的性质,其中根据二次不等式ax2+bx+c<0恒成立充要条件是a<0,△<0构造一个关于a的不等式,是解答本题的关键.

练习册系列答案
相关题目