题目内容
双曲线C：x2-y2=1的渐近线方程为 ；若双曲线C的右顶点为A，过A的直线l与双曲线C的两条渐近线交于P，Q两点，且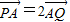
，则直线l的斜率为 ．
【答案】分析：把双曲线标准方程中的1，换成0，即得渐进性的方程；由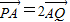
，可得A分PQ成的比为2，由定比分点坐标公式解方程求得直线l的斜率k的值．
解答：解：把双曲线C的标准方程：x2-y2=1中的1换成0，即得x±y=0，即为双曲线C：x2-y2=1的渐近线方程．
又A（1，0），设直线l的方程 y=k（x-1），
由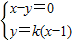
求得 P（
，
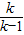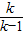），由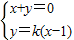
求得 Q （
，
）．
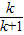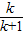由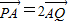
可得，A分PQ成的比为2，由定比分点坐标公式可得点A的横坐标1=
，
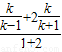解得 k=±3．
故答案为：x±y=0，±3．
点评：本题考查双曲线的标准方程以及简单性质的应用，求出P、Q两点的坐标，是解题的关键．
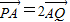，可得A分PQ成的比为2，由定比分点坐标公式解方程求得直线l的斜率k的值．解答：解：把双曲线C的标准方程：x2-y2=1中的1换成0，即得x±y=0，即为双曲线C：x2-y2=1的渐近线方程．
又A（1，0），设直线l的方程 y=k（x-1），
由
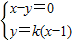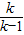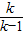求得 P（，），由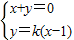求得 Q 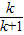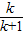（，）．由
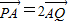可得，A分PQ成的比为2，由定比分点坐标公式可得点A的横坐标1=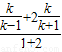，解得 k=±3．
故答案为：x±y=0，±3．
点评：本题考查双曲线的标准方程以及简单性质的应用，求出P、Q两点的坐标，是解题的关键．
练习册系列答案
教学练新同步练习系列答案
相关题目