题目内容
 如图在棱长为a的正方体ABCD-A1B1C1D1中,过A1C1B的平面与底面ABCD的交线为l,则直线l与A1C1的距离为
如图在棱长为a的正方体ABCD-A1B1C1D1中,过A1C1B的平面与底面ABCD的交线为l,则直线l与A1C1的距离为
| ||
| 2 |
| ||
| 2 |
分析:先证明l∥A1C1,再取A1C1的中点M,则所求距离为MB,利用勾股定理,即可得到结论.
解答: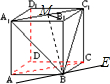 解:在平面ABCD内过点B作AC的平行线BE,
解:在平面ABCD内过点B作AC的平行线BE,
∵AC∥A1C1,AC∥BE,
∴BE∥A1C1,
∴面A1BC1与面ABCD的交线l与BE重合,即直线BE就是所求的直线l.
∵BE∥A1C1,l与BE重合,
∴l∥A1C1.
取A1C1的中点M,则所求距离为MB,
∵BB1=a,B1M=
a,
∴MB=
=
a
故答案为
a
 解:在平面ABCD内过点B作AC的平行线BE,
解:在平面ABCD内过点B作AC的平行线BE,∵AC∥A1C1,AC∥BE,
∴BE∥A1C1,
∴面A1BC1与面ABCD的交线l与BE重合,即直线BE就是所求的直线l.
∵BE∥A1C1,l与BE重合,
∴l∥A1C1.
取A1C1的中点M,则所求距离为MB,
∵BB1=a,B1M=
| ||
| 2 |
∴MB=
a2+
|
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题考查点到直线的距离,考查线面平行,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
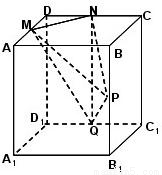
 现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开.
现有一块棱长为a的正方体形的木料,如图,M、N、P分别为AD、CD、BB1的中点.现要沿过M、N、P三点的平面将木料锯开. 内(含正方体表面)任取一点
内(含正方体表面)任取一点 ,则
,则 的概率
的概率 ( )
( )

 B.
B. C.
C. D.
D.
 内有一个内切球O,则过棱
内有一个内切球O,则过棱 和
和 的中点
的中点 、
、 的直线与球面交点为
的直线与球面交点为 、
、 ,则
,则 A.
A. B.
B. C.
C. D.
D. 
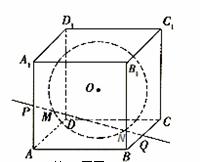 如图,在棱长为2的正方体
如图,在棱长为2的正方体 内有一个内切球O,则过棱
内有一个内切球O,则过棱 和
和 的中点
的中点 、
、 的直线与球面交点为
的直线与球面交点为 、
、 ,则
,则 B.
B.
 D.
D.