题目内容
已知直线
的参数方程是
（t为参数），圆C的极坐标为
（1）将圆C的极坐标方程化为直角坐标系方程；
（2）若圆上有且仅有三个点到直线的距离为
，求实数
的值.
的参数方程是（t为参数），圆C的极坐标为（1）将圆C的极坐标方程化为直角坐标系方程；
（2）若圆上有且仅有三个点到直线
的距离为，求实数的值.（1）
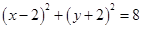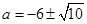
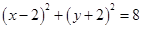；（2）
；（2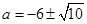）试题分析：(1)利用
将极坐标方程化为直角坐标方程，把展开，两边同时乘以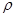
；（2）把直线的参数方程化为普通方程，在平面内到直线的距离为的点，在两条与平行且距离等于的平行线上，所以由题意圆与这两条平行线的公共点有三个，故圆心到直线的距离为，列式求.试题解析：(1)由
得，
，所以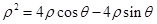
，∴
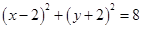，即圆C的直角坐标系方程为：；(2)将直线
的参数方程 化为普通方程为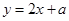
，则圆心C（2，-2）到直线的距离等于，即
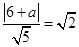，所以 .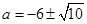
练习册系列答案
相关题目
（
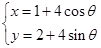为参数），直线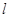
经过定点P（3，5），倾斜角为
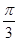（1）写出直线
的值
（
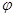为参数）的右焦点，斜率为
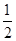的直线方程为 
上有3个不同的点到曲线
的距离等于2，则
.
中，过椭圆
的右焦点，且与直线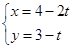
（
为参数）平行的直线截椭圆所得弦长为 ．
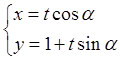(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
,求α的值.
（
为参数）的倾斜角的大小为（ ）
(
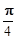
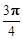
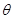为参数)化为普通方程是（ ）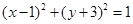
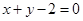
轴的正半轴重合，且长度单位相同．圆
的参数方程为
为参数），点
的极坐标为（
，
）．若点
是圆
两点间距离的最小值为 .