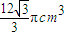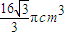题目内容
已知球的内接三棱锥的三条侧棱两两垂直,长度分别为3cm,2cm和
cm,则此球的体积为( )
| 3 |
分析:将三棱锥放入以3cm、2cm和
cm为长、宽和高的长方体中,则长方体与三棱锥有相同的外接球,利用长方体的对角线公式得到球直径,从而得到外接球的半径r,最后用球体积公式可求出该球的体积.
| 3 |
解答:解: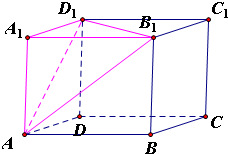 如图,将符合题意的三棱锥放入长方体ABCD-A1B1C1D1中,则三棱锥A1-AB1D1中,侧棱A1A、A1B1、A1D1互相垂直,
如图,将符合题意的三棱锥放入长方体ABCD-A1B1C1D1中,则三棱锥A1-AB1D1中,侧棱A1A、A1B1、A1D1互相垂直,
设长方体ABCD-A1B1C1D1的外接球为球O,则球O同时是三棱锥A1-AB1D1的外接球
∵长方体ABCD-A1B1C1D1的长、宽、高分别为3cm、2cm、
cm,
∴长方体的对角线长为
=4cm,
可得外接球O的半径为2cm.
根据球的体积公式,得球O的体积为V=
×r3=
πcm3
故选D
 如图,将符合题意的三棱锥放入长方体ABCD-A1B1C1D1中,则三棱锥A1-AB1D1中,侧棱A1A、A1B1、A1D1互相垂直,
如图,将符合题意的三棱锥放入长方体ABCD-A1B1C1D1中,则三棱锥A1-AB1D1中,侧棱A1A、A1B1、A1D1互相垂直,设长方体ABCD-A1B1C1D1的外接球为球O,则球O同时是三棱锥A1-AB1D1的外接球
∵长方体ABCD-A1B1C1D1的长、宽、高分别为3cm、2cm、
| 3 |
∴长方体的对角线长为
32+22+(
|
可得外接球O的半径为2cm.
根据球的体积公式,得球O的体积为V=
| 4π |
| 3 |
| 32 |
| 3 |
故选D
点评:本题给出三条侧棱两两垂直的三棱锥并给出三条侧棱的长,求三棱锥的外接球的体积,着重考查了球内接多面体、长方体对角线公式和球体积公式等知识,属于基础题.

练习册系列答案
相关题目
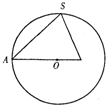 已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为
已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为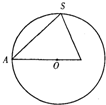 已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为________.
已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为________.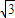 cm,则此球的体积为( )
cm,则此球的体积为( )