题目内容
为激发学生的学习兴趣,吴萱老师上课时在黑板上写出三个集合:A={x|x(△•x-1)<0},B={x|x2-3x-4≤0},C={x|log3x<-1};然后叫小南、小广、小郎三位同学到讲台上,并将“△”中的数告诉了他们,要求他们各用一句话来描述,以便同学们能确定该数.以下是小南、小广、小郎三位同学的描述:小南:此数为小于6的正整数; 小广:A是B成立的充分不必要条件; 小郎:A是C成立的必要不充分条件.若老师评说三位同学说的都对.
(Ⅰ)试求“△”中的数;
(Ⅱ)若D={x|x2+(a-8)x-8a≤0},求a的一个取值范围,使它成为A∩D=(0,
)一个必要不充分条件.
(Ⅰ)试求“△”中的数;
(Ⅱ)若D={x|x2+(a-8)x-8a≤0},求a的一个取值范围,使它成为A∩D=(0,
| 1 | 2 |
分析:(I)先求出两个集合B,C,再根据三位同学的描述确定集合A与两个集合B,C之间的关系,推测出△的可能取值;
(II)要求A∩D=(0,
)的必要不充分条件,即求一个a的一个取值集合M,使得A∩D=(0,
)的a的一个取值集合N?M.
(II)要求A∩D=(0,
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(I)由题意B={x|x2-3x-4≤0}={x|-1≤x≤4},C={x|log3x<-1}={x|0<x<
}
A={x|x(△•x-1)<0}={x|0<x<
}
由A是B成立的充分不必要条件知,A真包含于B,故
≤4,再由此数为小于6的正整数得出△≥
,
由A是C成立的必要不充分条件得出C包含于A,故
>
,得出△<3,
所以△=1或2;
(II)当△=1时,A={x|x(x-1)<0}={x|0<x<1},
D={x|x2+(a-8)x-8a≤0}={x|(x+a)(x-8)≤0},此时A∩D=(0,
)不可能成立,
当△=2时,A={x|x(2x-1)<0}={x|0<x<
},
D={x|x2+(a-8)x-8a≤0}={x|(x+a)(x-8)≤0},此时要使A∩D=(0,
)成立,
则-a<8,即a>-8,故D={x|-a≤x≤8},
当-a≤0时,即a≥0时,此时a的取值集合是A∩D=(0,
)一个必要不充分条件.
故所求的a的一个取值范围是[0.+∞).
| 1 |
| 3 |
A={x|x(△•x-1)<0}={x|0<x<
| 1 |
| △ |
由A是B成立的充分不必要条件知,A真包含于B,故
| 1 |
| △ |
| 1 |
| 4 |
由A是C成立的必要不充分条件得出C包含于A,故
| 1 |
| △ |
| 1 |
| 3 |
所以△=1或2;
(II)当△=1时,A={x|x(x-1)<0}={x|0<x<1},
D={x|x2+(a-8)x-8a≤0}={x|(x+a)(x-8)≤0},此时A∩D=(0,
| 1 |
| 2 |
当△=2时,A={x|x(2x-1)<0}={x|0<x<
| 1 |
| 2 |
D={x|x2+(a-8)x-8a≤0}={x|(x+a)(x-8)≤0},此时要使A∩D=(0,
| 1 |
| 2 |
则-a<8,即a>-8,故D={x|-a≤x≤8},
当-a≤0时,即a≥0时,此时a的取值集合是A∩D=(0,
| 1 |
| 2 |
故所求的a的一个取值范围是[0.+∞).
点评:本题考查必要条件、充分条件与充要条件的判断、集合中的参数取值问题,解题的关键是根据题设条件中三个同学的描述得出三个集合之间的包含关系,由这些关系得出所求的参数满足的条件,本题考查了推理论证的能力及运算能力.

练习册系列答案
相关题目
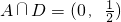 一个必要不充分条件.
一个必要不充分条件. 一个必要不充分条件.
一个必要不充分条件.