题目内容
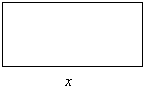 用长为20米的铁丝围成一个矩形框,设矩形的长为x,
用长为20米的铁丝围成一个矩形框,设矩形的长为x,(1)记矩形的面积为y,试将y表示为x的函数,并指出此函数的定义域;
(2)求当矩形的长和宽分别是多少时,矩形的面积y最大?并求出y的最大值.
分析:(1)求出矩形的高,然后根据面积公式即可求y.
(2)将二次函数进行配方,即可得到函数的最大值.
(2)将二次函数进行配方,即可得到函数的最大值.
解答:解:(1)∵矩形的长为x,
∴矩形的高为
=10-x,由10-x>0得0<x<10,
∴面积y=x(10-x)=-x2+10x,定义域为(0,10).
(2)y=-x2+10x=-(x-5)2+25,
∵0<x<10,
∴当x=5时,y取得最大值为25平方米
即当矩形的长和宽分别是5米,5米时,矩形的面积y最大,最大为25平方米.
∴矩形的高为
| 20-2x |
| 2 |
∴面积y=x(10-x)=-x2+10x,定义域为(0,10).
(2)y=-x2+10x=-(x-5)2+25,
∵0<x<10,
∴当x=5时,y取得最大值为25平方米
即当矩形的长和宽分别是5米,5米时,矩形的面积y最大,最大为25平方米.
点评:本题主要考查函数表达式的求法以及函数定义域的求法,利用二次函数的图象和性质是解决本题的关键,比较基础.

练习册系列答案
相关题目