Question

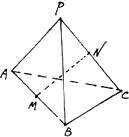
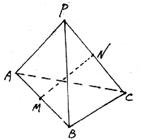
P是正角形ABC所在平面外一点，M、N分别是AB和PC的中点，且PA=PB=PC=AB=a．
（1）求证：MN是AB和PC的公垂线；
（2）求异面二直线AB和PC之间的距离．

Answer 1

分析：（1）连接AN，BN，证明MN⊥AB，MN⊥PC，MN∩AB=M，MN∩PC=N，即可求证：MN是AB和PC的公垂线；
（2）通过（1）等腰在角形ANB中，直接求出异面二直线AB和PC之间的距离．

解答：（1）证明：连接AN，BN，
∵△APC与△BPC是全等的正三角形，
又N是PC的中点
∴AN=BN
又∵M是AB的中点，∴MN⊥AB
同理可证MN⊥PC
又∵MN∩AB=M，MN∩PC=N
∴MN是AB和PC的公垂线；

（2）解：在等腰在角形ANB中，
∵AN=BN=

3

2

a，AB=a，
∴MN=

AN2-( 1 2 AB)2

=

2

2

a
即异面二直线AB和PC之间的距离为

2

2

a．

点评：本题考查用空间向量求直线间的夹角、距离，考查计算能力，转化思想，是中档题．