题目内容
如图，
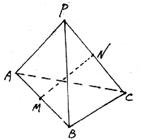
P是正角形ABC所在平面外一点，M、N分别是AB和PC的中点，且PA＝PB＝PC＝AB＝a．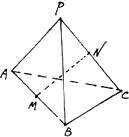
(1)求证：MN是AB和PC的公垂线
(2)求异面二直线AB和PC之间的距离
答案：
解析：
解析：
|
解析：(1)连结AN，BN，∵△APC与△BPC是全等的正三角形，又N是PC的中点 ∴ AN＝BN又∵M是AB的中点，∴MN⊥AB 同理可证MN⊥PC 又∵MN∩AB＝M，MN∩PC＝N ∴MN是AB和PC的公垂线． (2)在等腰在角形ANB中， 
即异面二直线AB和PC之间的距离为  ．
|
练习册系列答案
春雨教育同步作文系列答案
相关题目
