题目内容
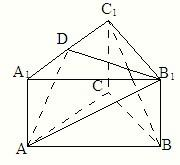
在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
(1)求证:AD⊥平面BC C1 B1;
(2)设E是B1C1上的一点,当![]() 的值为多少时,
的值为多少时,
A1E∥平面ADC1?请给出证明.
(1)见解析(2)1
解析:
(1)在正三棱柱中,C C1⊥平面ABC,AD![]() 平面ABC,
平面ABC,
∴ AD⊥C C1.
又AD⊥C1D,C C1交C1D于C1,且C C1和C1D都在面BC C1 B1内,
∴ AD⊥面BC C1 B1.
(2)由(1),得AD⊥BC.在正三角形ABC中,D是BC的中点.
当![]() ,即E为B1C1的中点时,A1E∥平面ADC1.
,即E为B1C1的中点时,A1E∥平面ADC1.
事实上,正三棱柱ABC-A1B1C1中,四边形BC C1 B1是矩形,且D、E分别是BC、B1C1的中点,所以B1B∥DE,B1B= DE.
又B1B∥AA1,且B1B=AA1,
∴DE∥AA1,且DE=AA1.所以四边形ADE A1为平行四边形,所以E A1∥AD.
而E A1![]() 面AD C1内,故A1E∥平面AD C1.
面AD C1内,故A1E∥平面AD C1.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为
如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为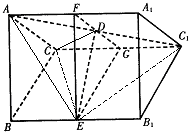 如图,在正三棱柱ABC-A1B1C1中,各棱长都等于a,D、E分别是AC1、BB1的中点,
如图,在正三棱柱ABC-A1B1C1中,各棱长都等于a,D、E分别是AC1、BB1的中点, 在正三棱柱ABC-A1B1C1中,AB=
在正三棱柱ABC-A1B1C1中,AB=