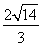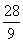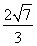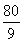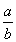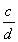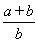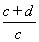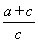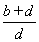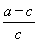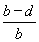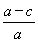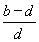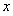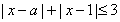题目内容
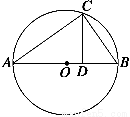
如图,已知Rt△ABC的周长为48 cm,一锐角平分线分对边为3∶5两部分.
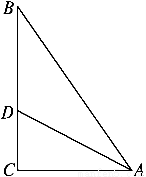
(1)求直角三角形的三边长;
(2)求两直角边在斜边上的射影的长.
(1) 20 cm,12 cm,16 cm (2) 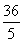 cm,
cm,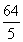 cm
cm
【解析】
解 (1)如图,设CD=3x,BD=5x,
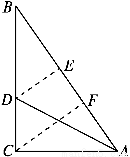
则BC=8x,
过D作DE⊥AB,
由Rt△ADC≌Rt△ADE可知,
DE=3x,BE=4x,
∴AE+AC+12x=48,
又AE=AC,
∴AC=24-6x,AB=24-2x,
∴(24-6x)2+(8x)2=(24-2x)2,
解得:x1=0(舍去),x2=2,
∴AB=20,AC=12,BC=16,
∴三边长分别为:20 cm,12 cm,16 cm.
(2)作CF⊥AB于F点,∴AC2=AF·AB,
∴AF=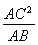 =
=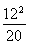 =
=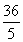 (cm);
(cm);
同理:BF=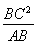 =
=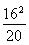 =
=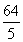 (cm).
(cm).
∴两直角边在斜边上的射影长分别为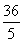 cm,
cm,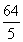 cm.
cm.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目