题目内容
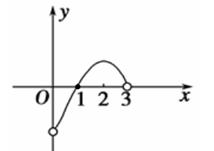
(12分)如图,A,B,C为函数 的图象
的图象
上的三点,它们的横坐标分别是t, t+2, t+4(t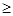 1).
1).
(1)设 ABC的面积为S 求S=f (t)
ABC的面积为S 求S=f (t)
(2)判断函数S=f (t)的单调性;
(3) 求S=f (t)的最大值.

 的图象
的图象上的三点,它们的横坐标分别是t, t+2, t+4(t
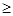 1).
1).(1)设
 ABC的面积为S 求S=f (t)
ABC的面积为S 求S=f (t) (2)判断函数S=f (t)的单调性;
(3) 求S=f (t)的最大值.

解:(1)过A,B,C,分别作AA1,BB1,CC1垂直于x轴,垂足为A1,B1,C1,
则S=S梯形AA1B1B+S梯形BB1C1C-S梯形AA1C1C.
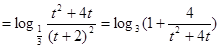 -------------------------------- 4分
-------------------------------- 4分
(2)因为v= 在
在 上是增函数,且v
上是增函数,且v 5,
5,
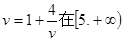 上是减函数,且1<u
上是减函数,且1<u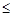
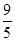 ; S
; S 上是增函数,
上是增函数,
所以复合函数S=f(t) 上是减函数-----------8分
上是减函数-----------8分
(3)由(2)知t=1时,S有最大值,最大值是f (1) -----------------------12分
则S=S梯形AA1B1B+S梯形BB1C1C-S梯形AA1C1C.
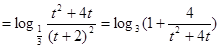 -------------------------------- 4分
-------------------------------- 4分(2)因为v=
 在
在 上是增函数,且v
上是增函数,且v 5,
5, 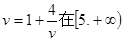 上是减函数,且1<u
上是减函数,且1<u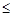
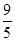 ; S
; S 上是增函数,
上是增函数,所以复合函数S=f(t)
 上是减函数-----------8分
上是减函数-----------8分(3)由(2)知t=1时,S有最大值,最大值是f (1) -----------------------12分
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的解的个数是( )
的解的个数是( )



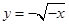 的图像为
的图像为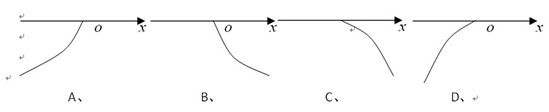
 ,
,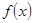 的第
的第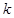 阶阶梯函数
阶阶梯函数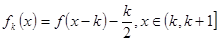 ,其中
,其中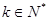 ,
,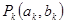 ,最低点
,最低点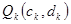
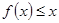 的解;
的解; 在某条直线
在某条直线 上.
上.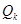 到(2)中的直线
到(2)中的直线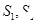 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,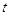 为时间,则与故事情节相吻合是
为时间,则与故事情节相吻合是 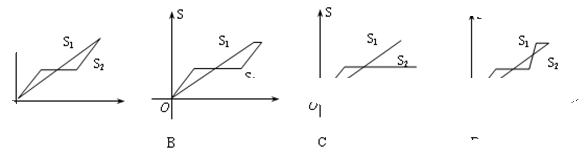
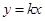 与
与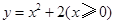 的图象相交于
的图象相交于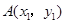 ,
,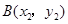 ,
,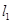 ,
,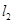 分别是
分别是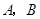 两点的切线,
两点的切线,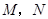 分别是
分别是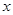 轴的交点.
轴的交点.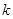 的取值范围;
的取值范围;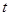 为点
为点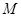 的横坐标,当
的横坐标,当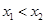 时,写出
时,写出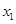 为自变量的函数式,并求其定义域和值域;
为自变量的函数式,并求其定义域和值域;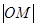 与
与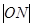 的大小,并说明理由(
的大小,并说明理由(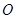 是坐标原点).
是坐标原点).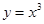 与
与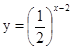 的图象的交点是
的图象的交点是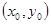 ,则
,则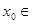 ( )
( )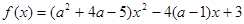 的图像全在
的图像全在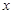 轴上方成立的充要条件.
轴上方成立的充要条件.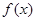 是定义在
是定义在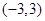 上的奇函数,当
上的奇函数,当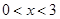 时,
时,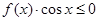 的解集为 .
的解集为 .