题目内容
△ABC所在平面上一点P满足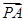 +
+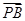 +
+ =
=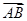 ,则△PAB的面积与△ABC的面积之比为
,则△PAB的面积与△ABC的面积之比为
| A.2∶3 | B.1∶3 | C.1∶4 | D.1∶6 |
B
解析试题分析:因为 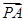 +
+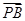 +
+ =
=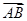 =
=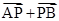
所以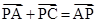 ,即
,即 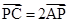
所以 A, P, C在同一直线,△PBC与 △ABC高一样,P为AC靠近点A的三等分点,
所以面积比= 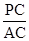 =1:3,故选B。
=1:3,故选B。
考点:本题主要考查平面向量的线性运算,共线向量。
点评:简单题,研究三角形面积之比,必定要研究三角形的边长关系,本题从证明三点共线、共线向量入手,达到明确边长关系、高的关系之目的。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
已知向量 满足
满足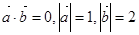 ,则
,则
| A.0 | B.2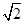 | C.4 | D.8 |
已知向量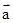 =(3,4),
=(3,4), =(2,-1),如果向量
=(2,-1),如果向量 与
与 垂直,则实数k的值为
垂直,则实数k的值为
A.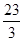 | B.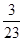 | C.2 | D.-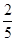 |
已知向量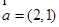 ,
, ,且
,且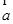 与
与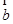 的夹角为锐角,则
的夹角为锐角,则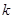 的取值范围是( )
的取值范围是( )
A. | B.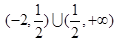 | C.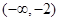 | D.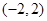 |
如图,在梯形ABCD中,AD∥BC,则 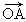 +
+ 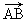 -
- 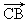 等于( )
等于( )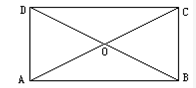
A.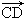 | B.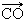 | C.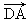 | D. |
设向量 ,若
,若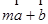 与
与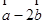 平行,则实数
平行,则实数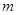 等于
等于
A. | B.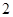 | C.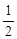 | D.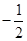 |
若第一象限内的点 ,落在经过点
,落在经过点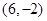 且具有方向向量
且具有方向向量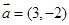 的直线
的直线 上,则
上,则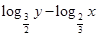 有 ( )
有 ( )
A.最大值 | B.最大值1 | C.最小值 | D.最小值1 |
若向量 、
、 满足
满足 =(2,-1),
=(2,-1), =(1,2),则向量
=(1,2),则向量 与
与 的夹角等于( )
的夹角等于( )
A. | B.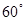 | C. | D. |
已知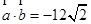 ,
,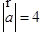 ,
,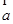 和
和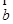 的夹角为
的夹角为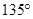 ,则
,则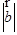 为( )
为( )
A.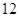 | B.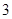 | C.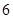 | D.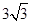 |