题目内容
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数如下表:
(1)已知两组技工在单位时间内加工的合格零件平均数为7,分别求出甲、乙两组技工在单位时间内加工的合格零件的方差,并由此分析两组技工的加工水平;
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工,对其加工的零件进行检测,若2人加工的合格零件个数之和超过14,则称该车间“质量合格”,求该车间“质量合格”的概率.
| | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲组 | 4 | 5 | x | 9 | 10 |
| 乙组 | 5 | 6 | 7 | y | 9 |
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工,对其加工的零件进行检测,若2人加工的合格零件个数之和超过14,则称该车间“质量合格”,求该车间“质量合格”的概率.
(1)两组技工水平基本相当,乙组更稳定些(2)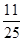
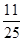
(1)由甲组技工在单位时间内加工的合格零件平均数 甲=
甲= (4+5+x+9+10)=7,得x=7.
(4+5+x+9+10)=7,得x=7.
由乙组技工在单位时间内加工的合格零件平均数
 乙=
乙= (5+6+7+y+9)=7,得y=8.
(5+6+7+y+9)=7,得y=8.
甲组方差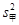 =
= [(4-7)2+(5-7)2+(7-7)2+(9-7)2+(10-7)2]=5.2.
[(4-7)2+(5-7)2+(7-7)2+(9-7)2+(10-7)2]=5.2.
乙组方差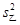 =
= [(5-7)2+(6-7)2+(7-7)2+(8-7)2+(9-7)2]=2.
[(5-7)2+(6-7)2+(7-7)2+(8-7)2+(9-7)2]=2.
∵ 甲=
甲= 乙,
乙,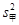 >
> 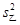 ,
,
∴两组技工水平基本相当,乙组更稳定些.
(2)从甲、乙两组中各随机抽取一名技工,加工的合格零件个数包含的基本事件为(4,5),(4,6),(4,7),(4,8),(4,9),(5,5),(5,6),(5,7),(5,8),(5,9),(7,5),(7,6),(7,7),(7,8),(7,9),(9,5),(9,6),(9,7),(9,8),(9,9),(10,5),(10,6),(10,7),(10,8),(10,9),共25个.
而车间“质量合格”包含的基本事件为(7,8),(7,9),(9,6),(9,7),(9,8),(9,9),(10,5),(10,6),(10,7),(10,8),(10,9),共11个,
因此,所求概率P=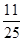 ,即该车间“质量合格”的概率为
,即该车间“质量合格”的概率为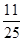 .
.
 甲=
甲= (4+5+x+9+10)=7,得x=7.
(4+5+x+9+10)=7,得x=7.由乙组技工在单位时间内加工的合格零件平均数
 乙=
乙= (5+6+7+y+9)=7,得y=8.
(5+6+7+y+9)=7,得y=8.甲组方差
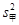 =
= [(4-7)2+(5-7)2+(7-7)2+(9-7)2+(10-7)2]=5.2.
[(4-7)2+(5-7)2+(7-7)2+(9-7)2+(10-7)2]=5.2.乙组方差
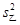 =
= [(5-7)2+(6-7)2+(7-7)2+(8-7)2+(9-7)2]=2.
[(5-7)2+(6-7)2+(7-7)2+(8-7)2+(9-7)2]=2.∵
 甲=
甲= 乙,
乙,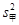 >
> 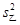 ,
, ∴两组技工水平基本相当,乙组更稳定些.
(2)从甲、乙两组中各随机抽取一名技工,加工的合格零件个数包含的基本事件为(4,5),(4,6),(4,7),(4,8),(4,9),(5,5),(5,6),(5,7),(5,8),(5,9),(7,5),(7,6),(7,7),(7,8),(7,9),(9,5),(9,6),(9,7),(9,8),(9,9),(10,5),(10,6),(10,7),(10,8),(10,9),共25个.
而车间“质量合格”包含的基本事件为(7,8),(7,9),(9,6),(9,7),(9,8),(9,9),(10,5),(10,6),(10,7),(10,8),(10,9),共11个,
因此,所求概率P=
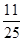 ,即该车间“质量合格”的概率为
,即该车间“质量合格”的概率为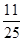 .
.
练习册系列答案
相关题目

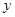 (吨)与气温
(吨)与气温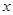 (℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表:
(℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表: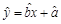 中的
中的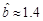 ,试求出
,试求出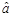 的值,并预测当地气温为5℃时,该生活小区的用水量.
的值,并预测当地气温为5℃时,该生活小区的用水量. 上,将这些成绩分成六段
上,将这些成绩分成六段 ,
, ,…
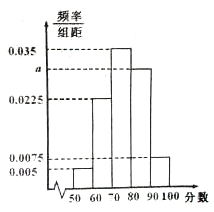
,… ,后得到如图所示部分频率分布直方图.
,后得到如图所示部分频率分布直方图.
 内的人数;(5分)
内的人数;(5分) 的列联表如下:
的列联表如下: ;
;






 +
+ +
+ +
+ =
= ,365=73×5).
,365=73×5).
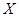 为学校因为该学员而奖励教官的金额数,求
为学校因为该学员而奖励教官的金额数,求