题目内容
函数f(x)=Asin(ωx+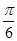 )(ω>0)的图像与x轴交点的横坐标构成一个公差为
)(ω>0)的图像与x轴交点的横坐标构成一个公差为 的等差数列,要得到函数g(x)=Acosωx的图象,只需将f(x)的图像 ( )
的等差数列,要得到函数g(x)=Acosωx的图象,只需将f(x)的图像 ( )
A.向左平移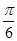 个单位 个单位 | B.向右平移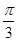 个单位 个单位 |
C.向左平移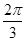 个单位 个单位 | D.向右平移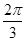 个单位 个单位 |
A
解析试题分析:由题设知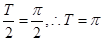 ,又因为
,又因为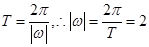 ,而
,而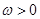 ,所以
,所以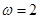
所以,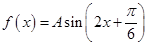 =
=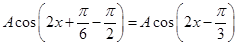 ,因为
,因为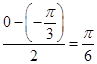
所以,要得到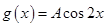 的图象,只需将
的图象,只需将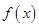 的图象向左平移
的图象向左平移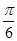 个单位.
个单位.
故选A.
考点:1、三解函数的图象与性质;2、三角函数的图象变换;3、诱导公式.

练习册系列答案
相关题目
为了得到函数 的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( )
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
如图,在直角坐标系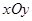 中,射线OP交单位圆O于点P,若∠XOP =θ,则点P的坐标是( ).
中,射线OP交单位圆O于点P,若∠XOP =θ,则点P的坐标是( ).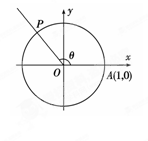
| A.(cosθ,sinθ) | B.(-cosθ,sinθ) |
| C.(sinθ,cosθ) | D.(-sinθ,cosθ) |
已知函数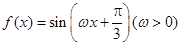 的最小正周期为
的最小正周期为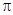 ,则该函数的图象( )
,则该函数的图象( )
A.关于点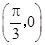 对称 对称 | B.关于直线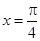 对称 对称 |
C.关于点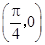 对称 对称 | D.关于直线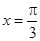 对称 对称 |
函数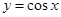 的一个单调递增区间为 ( )
的一个单调递增区间为 ( )
A.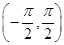 | B.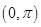 | C. | D.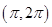 |
已知MP,OM,AT分别为角
 的正弦线、余弦线、正切线,则一定有( )
的正弦线、余弦线、正切线,则一定有( )
A. | B. |
C. | D. |
函数 的图象的一条对称轴方程是( ).
的图象的一条对称轴方程是( ).
A.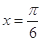 | B.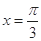 | C.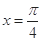 | D.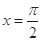 |
在函数① ,②
,② ,③
,③ ,④
,④ 中,最小正周期为
中,最小正周期为 的所有函数为
的所有函数为
| A.①②③ | B.①③④ | C.②④ | D.①③ |
已知函数y=Asin(ωx+φ)+k的最大值是4,最小值是0,最小正周期是 ,直线x=
,直线x= 是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
A.y=4sin(4x+ ) ) | B.y=2sin(2x+ )+2 )+2 |
C.y=2sin(4x+ )+2 )+2 | D.y=2sin(4x+ )+2 )+2 |