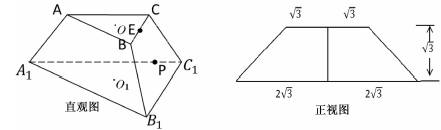
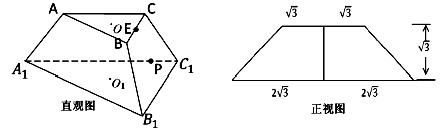题目内容
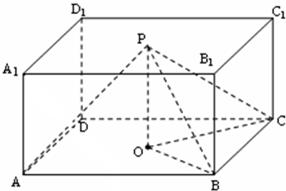
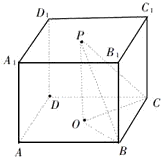 如图,O,P分别是正方体ABCD-A1B1C1D1底面的中心,连接PB,PC,OB,OC和OP.
如图,O,P分别是正方体ABCD-A1B1C1D1底面的中心,连接PB,PC,OB,OC和OP.
(1)求证:平面PBO⊥平面PCO
(2)求直线B1C1与平面POB所成的角.
解: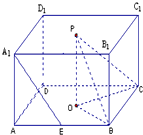 (1)证明:∵ABCD是正方形,O为中心,∴BO⊥OC,
(1)证明:∵ABCD是正方形,O为中心,∴BO⊥OC,
∵O,P分别是正方体ABCD-A1B1C1D1底面的中心,
∴PO⊥平面ABCD,∴PO⊥OB,
∴OB⊥平面PCO,(3分)
又∵OB?平面PBO,∴平面PBO⊥平面PCO; (2分)
(2)∵B1C1∥BC,
∴直线B1C1与平面POB所成的角等于直线BC与平面POB所成的角
∵平面PBO⊥平面PCO,OC⊥OB,∴OC⊥平面POB,
∠CBO就是B1C1与平面POB所成的角.(3分)
在△CBO中,∠CBO= .所以直线B1C1与平面POB所成的角为
.所以直线B1C1与平面POB所成的角为 .(2分)
.(2分)
分析:(1)根据已知中ABCD是正方形,O,P分别是正方体ABCD-A1B1C1D1底面的中心,则BO⊥OC,PO⊥OB,则由线面垂直的判定定理可得OB⊥平面PCO,再由面面垂直的判定定理,即可得到平面PBO⊥平面PCO
(2)由正方体的几何特征得B1C1∥BC,直线B1C1与平面POB所成的角等于直线BC与平面POB所成的角,即∠CBO就是B1C1与平面POB所成的角,解三角形CBO即可得到答案.
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面所成的角,其中(1)的关键是要判断出OB⊥平面PCO,(2)的关键是找出∠CBO就是B1C1与平面POB所成的角.
 (1)证明:∵ABCD是正方形,O为中心,∴BO⊥OC,
(1)证明:∵ABCD是正方形,O为中心,∴BO⊥OC,∵O,P分别是正方体ABCD-A1B1C1D1底面的中心,
∴PO⊥平面ABCD,∴PO⊥OB,
∴OB⊥平面PCO,(3分)
又∵OB?平面PBO,∴平面PBO⊥平面PCO; (2分)
(2)∵B1C1∥BC,
∴直线B1C1与平面POB所成的角等于直线BC与平面POB所成的角
∵平面PBO⊥平面PCO,OC⊥OB,∴OC⊥平面POB,
∠CBO就是B1C1与平面POB所成的角.(3分)
在△CBO中,∠CBO=
 .所以直线B1C1与平面POB所成的角为
.所以直线B1C1与平面POB所成的角为 .(2分)
.(2分)分析:(1)根据已知中ABCD是正方形,O,P分别是正方体ABCD-A1B1C1D1底面的中心,则BO⊥OC,PO⊥OB,则由线面垂直的判定定理可得OB⊥平面PCO,再由面面垂直的判定定理,即可得到平面PBO⊥平面PCO
(2)由正方体的几何特征得B1C1∥BC,直线B1C1与平面POB所成的角等于直线BC与平面POB所成的角,即∠CBO就是B1C1与平面POB所成的角,解三角形CBO即可得到答案.
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面所成的角,其中(1)的关键是要判断出OB⊥平面PCO,(2)的关键是找出∠CBO就是B1C1与平面POB所成的角.

练习册系列答案
相关题目
 如图,P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,AB=kAA1.
如图,P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,AB=kAA1. 如图,已知P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,E是AB的中点,AB=kAA1,其中k为非零实数,
如图,已知P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,E是AB的中点,AB=kAA1,其中k为非零实数,