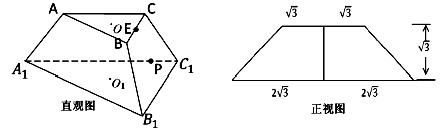题目内容
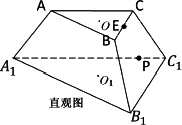
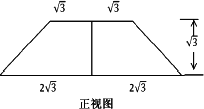
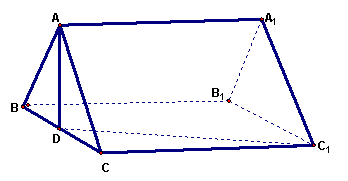
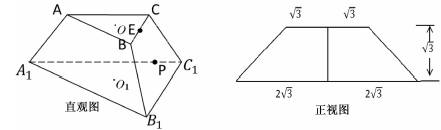
(13分)如图分别是正三棱台ABC-A1B1C1的直观图和正视图,O,O1分别是上下底面的中心,E是BC中点.
(1)求正三棱台ABC-A1B1C1的体积;
(2)求平面EA1B1与平面A1B1C1的夹角的余弦;
(3)若P是棱A1C1上一点,求CP+PB1的最小值.
【答案】
(1)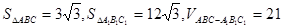 ;
;
(2)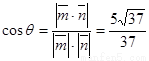 ;(3)
;(3) 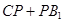 的最小值为
的最小值为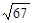
【解析】本试题主要是考查了立体几何中二面角的求解和棱台体积公式的运用,以及线段和的最值问题的综合运用。
(1)首先要求解三棱台的体积,关键是高度和底面积,然后结合公式得到。
(2)建立适当的空间直角坐标系,表示出点的坐标和向量的坐标,进而求解二面角的平面角的问题。
(3)结合三角形的知识,求解两边的和的最小值,要借助于余弦定理得到。
解:(1)由题意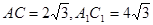 ,正三棱台高为
,正三棱台高为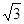 ……..2分
……..2分
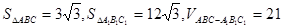 ………..4分
………..4分
(2)设 分别是上下底面的中心,
分别是上下底面的中心,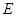 是
是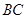 中点,
中点,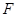 是
是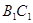 中点.
中点.
如图,建立空间直角坐标系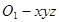 .
. 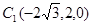 ,
,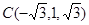 ,
,
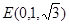 ,
,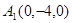 ,
,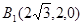 ,
,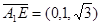 ,
,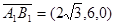 ,
,

设平面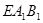 的一个法向量
的一个法向量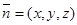 ,则
,则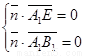 即
即
取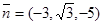 ,取平面
,取平面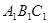 的一个法向
的一个法向
量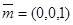 ,设所求角为
,设所求角为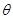
则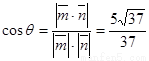 ……..8分
……..8分
(3)将梯形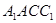 绕
绕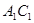 旋转到
旋转到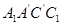 ,使其与
,使其与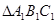 成平角
成平角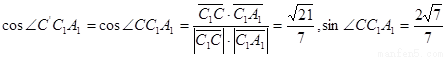
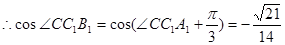
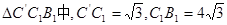 ,由余弦定理得
,由余弦定理得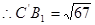
即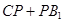 的最小值为
的最小值为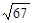 ……..13分
……..13分


练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目