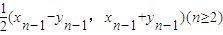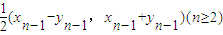题目内容
已知一非零向量列{an}满足:a1=(1,1),an=(xn,yn)=
(1)证明:{|an|}是等比数列;
(2)设θn=<a n-1,an>(n≥2),bn=2nθn-1,Sn=b1+b2+…+bn,求Sn;
(3)设cn=|an|log2|an|,问数列{cn}中是否存在最小项?若存在,求出最小项;若不存在,请说明理由.
【答案】分析:(1)先利用向量模的计算公式得出 的表达式,发现得出
的表达式,发现得出 =
= 利用等比数列定义判定是等比数列.
利用等比数列定义判定是等比数列.
(2)根据向量夹角公式可以求出θn= ,bn=2nθn-1=
,bn=2nθn-1= .分组后结合等差数列求和公式计算.
.分组后结合等差数列求和公式计算.
(3)由上可得出cn= •
• ,可利用作商法研究数列{cn}的单调性,确定最小项存在与否.
,可利用作商法研究数列{cn}的单调性,确定最小项存在与否.
解答:解:(l)证明: =
=

=
 =
= (n≥2)又
(n≥2)又 =
=
∴数列 是以
是以 为首项,公比为
为首项,公比为 的等比数列.…(4分)
的等比数列.…(4分)
(2)∵ =
= =
= =
= 2
2
∴cosθn= =
= ,∴θn=
,∴θn= ,∴bn=2nθn-1=
,∴bn=2nθn-1= .
.
Sn=b1+b2+…+bn= =
= …(8分)
…(8分)
(3)假设存在最小项,不防设为cn,∵ =
= =
= ,
,
∴cn=|an|log2|an|= •
• ,由cn≤cn+1 得
,由cn≤cn+1 得 ≤
≤
即 (2-n)≤1-n,∴(
(2-n)≤1-n,∴( -1)n≥2
-1)n≥2 -1.
-1.
∴n≥ =3+
=3+ ,∵n为正整数,∴n≥5.
,∵n为正整数,∴n≥5.
由cn≤cn-1 得n≤4+ ,n≤5.,∴n=5
,n≤5.,∴n=5
故存在最小项,最小项为c5= …(12分)
…(12分)
点评:本题考查数列的函数性质,等比数列的判定,数列求和,向量数量积、夹角的计算,是数列与不等式的综合.所涉及的知识、方法均为高中学段基本要求.
 的表达式,发现得出
的表达式,发现得出 =
= 利用等比数列定义判定是等比数列.
利用等比数列定义判定是等比数列.(2)根据向量夹角公式可以求出θn=
 ,bn=2nθn-1=
,bn=2nθn-1= .分组后结合等差数列求和公式计算.
.分组后结合等差数列求和公式计算.(3)由上可得出cn=
 •
• ,可利用作商法研究数列{cn}的单调性,确定最小项存在与否.
,可利用作商法研究数列{cn}的单调性,确定最小项存在与否.解答:解:(l)证明:
 =
=

=

 =
= (n≥2)又
(n≥2)又 =
=
∴数列
 是以
是以 为首项,公比为
为首项,公比为 的等比数列.…(4分)
的等比数列.…(4分)(2)∵
 =
= =
= =
= 2
2∴cosθn=
 =
= ,∴θn=
,∴θn= ,∴bn=2nθn-1=
,∴bn=2nθn-1= .
.Sn=b1+b2+…+bn=
 =
= …(8分)
…(8分)(3)假设存在最小项,不防设为cn,∵
 =
= =
= ,
,∴cn=|an|log2|an|=
 •
• ,由cn≤cn+1 得
,由cn≤cn+1 得 ≤
≤
即
 (2-n)≤1-n,∴(
(2-n)≤1-n,∴( -1)n≥2
-1)n≥2 -1.
-1.∴n≥
 =3+
=3+ ,∵n为正整数,∴n≥5.
,∵n为正整数,∴n≥5.由cn≤cn-1 得n≤4+
 ,n≤5.,∴n=5
,n≤5.,∴n=5故存在最小项,最小项为c5=
 …(12分)
…(12分)点评:本题考查数列的函数性质,等比数列的判定,数列求和,向量数量积、夹角的计算,是数列与不等式的综合.所涉及的知识、方法均为高中学段基本要求.

练习册系列答案
相关题目