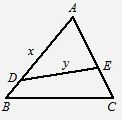题目内容
在边长为1的等边三角形ABC中,设
=2
,
=3
(1)用向量
,
作为基底表示向量
(2)求
•
.
| BC |
| BD |
| CA |
| CE |
(1)用向量
| AB |
| AC |
| BE |
(2)求
| AD |
| BE |
分析:(1)根据
=3
可得
=
,再根据
=
+
可用向量
,
作为基底表示向量
;
(2)根据
•
=
(-
+
)=
•(-
)+
•
,然后利用数量积公式可求出所求.
| CA |
| CE |
| AE |
| 2 |
| 3 |
| AC |
| BE |
| BA |
| AE |
| AB |
| AC |
| BE |
(2)根据
| AD |
| BE |
| AD |
| AB |
| 2 |
| 3 |
| AC |
| AD |
| AB |
| AD |
| 2 |
| 3 |
| AC |
解答:解:(1)∵
=3
∴
=
∴
=
+
=-
+
------------(4分)
(2)
•
=
(-
+
)=
•(-
)+
•
---(6分)
=|
|•|
|cos150°+
|
|•|
|cos30°----------(9分)
=
×1×(-
)+
×
×1×
=-
-----------(12分)
| CA |
| CE |
∴
| AE |
| 2 |
| 3 |
| AC |
∴
| BE |
| BA |
| AE |
| AB |
| 2 |
| 3 |
| AC |
(2)
| AD |
| BE |
| AD |
| AB |
| 2 |
| 3 |
| AC |
| AD |
| AB |
| AD |
| 2 |
| 3 |
| AC |
=|
| AD |
| AB |
| 2 |
| 3 |
| AD |
| AC |
=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
点评:本题主要考查了平面向量数量积的运算,以及向量的线性表示,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
 形状的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
形状的三角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.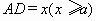 ,
,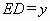 ,求用
,求用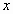 表示
表示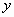 的函数关系式.
的函数关系式.