题目内容
在正方形ABCD中,E、F分别为AB、BC的中点,现在沿DE、DF及EF把△ADE、△CDF和△BEF折起,使A、B、C三点重合,重合后的点记为P.问:
①依据题意画出这个几何体;
②这个几何体由哪几个面构成,每个面的三角形是什么三角形;
③若正方形边长为2a,则每个面的三角形面积为多少.
①依据题意画出这个几何体;
②这个几何体由哪几个面构成,每个面的三角形是什么三角形;
③若正方形边长为2a,则每个面的三角形面积为多少.
分析:①这个几何体是一个四边体;
②这个几何体由四个面构成,即面DEF、面DFP、面DEP、面EFP.由平几知识,∠DPE=∠EPF=∠DPF=90°,从而判断△DEF,△DFP、△EFP、△DEP的形状.
③由②可知,DE=DF=
a,EF=
a,利用三角形的面积公式即可求得每个面的三角形面积.
②这个几何体由四个面构成,即面DEF、面DFP、面DEP、面EFP.由平几知识,∠DPE=∠EPF=∠DPF=90°,从而判断△DEF,△DFP、△EFP、△DEP的形状.
③由②可知,DE=DF=
| 5 |
| 2 |
解答: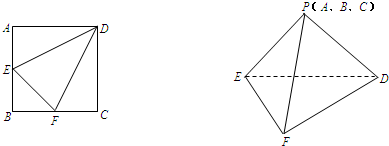 解:①如图所示.
解:①如图所示.
②这个几何体由四个面构成,即面DEF、面DFP、面DEP、面EFP.
由平几知识可知DE=DF,∠DPE=∠EPF=∠DPF=90°,
所以△DEF为等腰三角形,△DFP、△EFP、△DEP为直角三角形.
③由②可知,DE=DF=
a,EF=
a,所以,S△DEF=
a2.DP=2a,EP=FP=a,
所以S△DPE=S△DPF=a2,S△EPF=
a2.
 解:①如图所示.
解:①如图所示.②这个几何体由四个面构成,即面DEF、面DFP、面DEP、面EFP.
由平几知识可知DE=DF,∠DPE=∠EPF=∠DPF=90°,
所以△DEF为等腰三角形,△DFP、△EFP、△DEP为直角三角形.
③由②可知,DE=DF=
| 5 |
| 2 |
| 3 |
| 2 |
所以S△DPE=S△DPF=a2,S△EPF=
| 1 |
| 2 |
点评:本小题主要考查棱锥的结构特征,三角形面积和线面关系等基本知识,同时考查空间想象能力和推理、运算能力.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
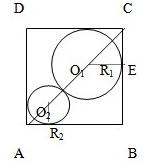 如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.
如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆. 在正方形ABCD中,E、F分别为AB、BC的中点,用向量求证:AF⊥DE.
在正方形ABCD中,E、F分别为AB、BC的中点,用向量求证:AF⊥DE. 如图,在正方形ABCD中,M是边BC的中点,N是边CD的中点,设∠MAN=α,那么sinα的值等于
如图,在正方形ABCD中,M是边BC的中点,N是边CD的中点,设∠MAN=α,那么sinα的值等于 (2012•武汉模拟)如图,在正方形ABCD中,点E为CD的中点,点F为BC上靠近点B的一个三等分点,则
(2012•武汉模拟)如图,在正方形ABCD中,点E为CD的中点,点F为BC上靠近点B的一个三等分点,则