题目内容
已知直线l过点M(-3,-3),圆N:x2+y2+4y-21=0,l被圆N所截得的弦长为4
.
(1)求点N到直线l的距离;
(2)求直线l的方程.
| 5 |
(1)求点N到直线l的距离;
(2)求直线l的方程.
分析:(1)设直线l与圆N交于A和B两点,过N作ND垂直于AB,根据垂径定理得到D为AB中点,把圆N的方程化为标准方程,找出圆心N的坐标和半径r,由|AB|的长,得到|DB|的长,再由半径r的值,利用勾股定理求出|ND|的长,即为N到直线l的距离;
(2)若直线l的斜率不存在,即直线l的方程为x=-3,求出此时|AB|的长,发现与已知的弦长不相等,推出矛盾,故直线l的斜率存在,设直线l的斜率为k,再根据直线l过M点,表示出直线l的方程,由(1)得到N到直线l的距离,再利用点到直线的距离公式表示出圆心N到设出的直线l的距离,进而列出关于k的方程,求出方程的解得到k的值,即可确定出直线l的方程.
(2)若直线l的斜率不存在,即直线l的方程为x=-3,求出此时|AB|的长,发现与已知的弦长不相等,推出矛盾,故直线l的斜率存在,设直线l的斜率为k,再根据直线l过M点,表示出直线l的方程,由(1)得到N到直线l的距离,再利用点到直线的距离公式表示出圆心N到设出的直线l的距离,进而列出关于k的方程,求出方程的解得到k的值,即可确定出直线l的方程.
解答: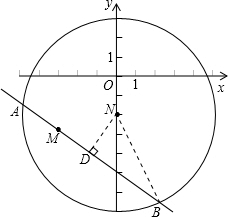 解:(1)设直线l与圆N交于A,B两点(如图)
解:(1)设直线l与圆N交于A,B两点(如图)
作ND⊥AB交直线l于点D,显然D为AB的中点,…(2分)
由x2+y2+4y-21=0化为标准方程得:x2+(y+2)2=25,
∴圆心N(0,-2),r=5,…(4分)又|AB|=4
,
∴|ND|=
=
,即点N到直线l的距离为
;…(6分)
(2)若直线l的斜率不存在,则直线l的方程为x=-3,
∴N到l的距离为3,又圆N的半径为5,
易知
=4,即|AB|=8≠4
,不符合题意,
故直线l的斜率存在;…(8分)
于是设直线l的方程为:y+3=k(x+3),即kx-y+3k-3=0,
∴圆心N(0,-2)到直线l的距离d=
=
,①
由(1)知,d=
,②…(10分)
由①②可以得到k=2,或k=-
,
则直线l的方程为2x-y+3=0或x+2y+9=0.…(12分)
 解:(1)设直线l与圆N交于A,B两点(如图)
解:(1)设直线l与圆N交于A,B两点(如图)作ND⊥AB交直线l于点D,显然D为AB的中点,…(2分)
由x2+y2+4y-21=0化为标准方程得:x2+(y+2)2=25,
∴圆心N(0,-2),r=5,…(4分)又|AB|=4
| 5 |
∴|ND|=
r2-(
|
| 5 |
| 5 |
(2)若直线l的斜率不存在,则直线l的方程为x=-3,
∴N到l的距离为3,又圆N的半径为5,
易知
| |AB| |
| 2 |
| 5 |
故直线l的斜率存在;…(8分)
于是设直线l的方程为:y+3=k(x+3),即kx-y+3k-3=0,
∴圆心N(0,-2)到直线l的距离d=
| |-(-2)+3k-3| | ||
|
| |3k-1| | ||
|
由(1)知,d=
| 5 |
由①②可以得到k=2,或k=-
| 1 |
| 2 |
则直线l的方程为2x-y+3=0或x+2y+9=0.…(12分)
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,垂径定理,勾股定理,点到直线的距离公式,直线的点斜式方程,利用了分类讨论及数形结合的数学思想,是一道综合性较强的中档题.当直线与圆相交时,常常由作出弦心距,利用垂径定理得到垂足为弦的中点,进而由弦心距,弦长的一半及圆的半径构造直角三角形,利用勾股定理来解决问题.

练习册系列答案
相关题目
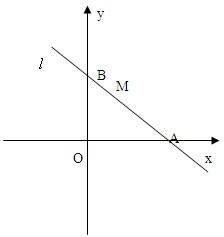 已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上)
已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上)