题目内容
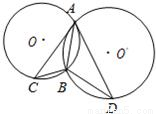
如图圆O和圆O′相交于A，B两点，AC是圆O′的切线，AD是圆O的切线，若BC=2，AB=4，求BD．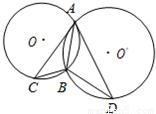
【答案】分析：先利用圆的切线的性质，结合弦切角定理得到两个三角形△CBA、△BAD中的两组角相等，从而证得它们相似，得到一个比例式：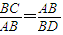
，由此求得BD的长即可．
解答：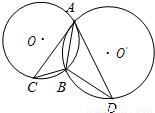
解：∵AC是圆O′的切线，
∴∠CAB=∠BDA，
又AD是圆O的切线，
∴∠BCA=∠BAD，
∴△CBA∽△BAD，（5分）
所以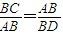
，
即：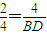
BD=8（10分）．
点评：本题考查的与圆有关的比例线段、切线的性质及相似三角形的判定和性质等的综合运用．
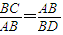，由此求得BD的长即可．解答：
解：∵AC是圆O′的切线，∴∠CAB=∠BDA，
又AD是圆O的切线，
∴∠BCA=∠BAD，
∴△CBA∽△BAD，（5分）
所以
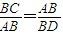，即：
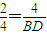
BD=8（10分）．
点评：本题考查的与圆有关的比例线段、切线的性质及相似三角形的判定和性质等的综合运用．
练习册系列答案
相关题目
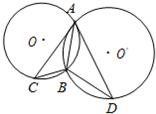如图圆O和圆O′相交于A，B两点，AC是圆O′的切线，AD是圆O的切线，若BC=2，AB=4，求BD．
如图圆O和圆O′相交于A，B两点，AC是圆O′的切线，AD是圆O的切线，若BC=2，AB=4，求BD．
