题目内容
14.已知函数f(x)=loga(x2-2ax)在区间[4,5]上是增函数,则实数a的取值范围是(1,2).分析 由题意可得g(x)=x2-2ax的对称轴为x=a,①当a>1时,由复合函数的单调性可知,g(x)在[4,5]单调递增,且g(x)>0在[4,5]恒成立,②0<a<1时,由复合函数的单调性可知,g(x)在[4,5]单调递增,且g(x)>0在[4,5]恒成立从而可求a.
解答 解:由题意可得g(x)=x2-2ax的对称轴为x=a
①当a>1时,由复合函数的单调性可知,g(x)在[4,5]单调递增,且g(x)>0在[4,5]恒成立
则$\left\{\begin{array}{l}a>1\\ g(4)=16-8a>0\\ a≤4\end{array}\right.$
∴1<a<2
②0<a<1时,由复合函数的单调性可知,g(x)在[4,5]单调递增,且g(x)>0在[4,5]恒成立
则$\left\{\begin{array}{l}0<a<1\\ a≥5\\ g(5)=25-10a>0\end{array}\right.$此时a不存在
综上可得,1<a<2.
故答案为:(1,2).
点评 本题主要考查了由对数函数及二次函数复合二次的复合函数的单调性的应用,解题中一定要注意对数的真数大于0这一条件的考虑.

练习册系列答案
相关题目
4.如图,设正方体ABCD-A1B1C1D1的棱长为1,则直线B1C与平面AB1D1所成的角的正弦值是( )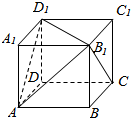

| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
6.已知α是第二象限角,tan(π+α)=-$\frac{8}{15}$,则cos(α-$\frac{π}{2}$)=( )
| A. | $\frac{1}{8}$ | B. | -$\frac{1}{8}$ | C. | $\frac{8}{17}$ | D. | -$\frac{8}{17}$ |
 如图,已知四边形ABCD为正方形,SA⊥AB,SA⊥AC,AC与BD的交点为O,AB=2$\sqrt{2}$cm,SC=5cm.
如图,已知四边形ABCD为正方形,SA⊥AB,SA⊥AC,AC与BD的交点为O,AB=2$\sqrt{2}$cm,SC=5cm.