题目内容
已知e是自然对数底数,若函数y=
的定义域为R,则实数a的取值范围为( )
| e |
| ex-x+a |
| A.a<-1 | B.a≤-1 | C.a>-1 | D.a≥-1 |
∵e是自然对数底数,若函数y=
的定义域为R,
∴ex-x+a>0,在R上恒成立,
令f(x)=ex-x,只要求出f(x)的最小值即可,
∴f′(x)=ex-1=0,解得x=0,
∴f(x)的最小值为f(0)=1,
∴1+a>0,
∴a>-1,
故选C.
| e |
| ex-x+a |
∴ex-x+a>0,在R上恒成立,
令f(x)=ex-x,只要求出f(x)的最小值即可,
∴f′(x)=ex-1=0,解得x=0,
∴f(x)的最小值为f(0)=1,
∴1+a>0,
∴a>-1,
故选C.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知e是自然对数底数,若函数y=
的定义域为R,则实数a的取值范围为( )
| e |
| ex-x+a |
| A、a<-1 | B、a≤-1 |
| C、a>-1 | D、a≥-1 |
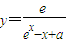 的定义域为R,则实数a的取值范围为( )
的定义域为R,则实数a的取值范围为( ) 的定义域为R,则实数a的取值范围为( )
的定义域为R,则实数a的取值范围为( )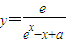 的定义域为R,则实数a的取值范围为( )
的定义域为R,则实数a的取值范围为( )