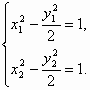题目内容
A、B是双曲线
＝1上的两点，点N(1，2)是线段AB的中点．
(1)求直线AB的方程；
(2)若线段AB的垂直平分线交双曲线于C、D两点，那么A、B、C、D四点是否共圆，为什么？
答案：
解析：
解析：
|
解法一：(1)由于直线AB与x轴不垂直，故可设其斜率为k，则方程为：y＝k(x－1)＋2． 代入双曲线方程消x并整理得：(2－k2)x2－2k(2－k)x－k2＋4k－6＝0． 设A(x1，y1)，B(x2，y2)，由 (2)AB的垂直平分线方程为x＋y－3＝0，代入双曲线根据弦长公式求得|CD|＝ 解法二：设A(x1，y1)，B(x2，y2)，代入双曲线得 作差得 解法二通常称之为“点差法”，同学们可以尝试一下已知曲线为椭圆或抛物线的情形．此外，本题也可根据椭圆的参数方程设点B的坐标，化为三角函数求出最大值，感兴趣者不妨一试． 分析：直线与圆锥曲线的关系问题是高考重点考查内容，常需联立方程，消元后运用根与系数关系，此外还可考虑“点差法”． |
，解得k＝1，从而直线方程为x－y＋1＝0．
，CD中点M(－3，6)．又|AM|＝|BM|＝
，故四点共圆．
＝1，即k＝1，以下同解法一．
练习册系列答案
相关题目
＝1上一点，双曲线的一条渐近线方程为3x－2y＝0，F1、F2分别是双曲线的左、右焦点．若|PF1|＝3，则|PF2|＝
＝1上一点，双曲线的一条渐近线方程为3x－2y＝0，点F1、F2分别是双曲线的左、右焦点．若PF1＝3，则PF2＝
＝1上的两点，点N(1，2)是线段AB的中点．
＝1上一点，双曲线的一条渐近线方程为3x－2y＝0，F1、F2分别是双曲线的左、右焦点，若|PF1|＝3，则|PF2|＝