题目内容
已知函数 (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
.(1)求f(x)的解析式;
(2)若
 求函数f(x)的值域;
求函数f(x)的值域;(3)将函数y=f(x)的图象向左平移
 个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.
个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.
【答案】分析:(1)根据已知可求出函数的周期,进而求出ω值,代入点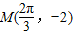 可得A值,进而求出f(x)的解析式;
可得A值,进而求出f(x)的解析式;
(2)由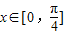 可求出相位角的取值范围,结合正弦函数的性质可得此时函数f(x)的值域;
可求出相位角的取值范围,结合正弦函数的性质可得此时函数f(x)的值域;
(3)根据(1)中函数的解析式,结合函数图象的平移变换法则及伸缩变换法则,可得变换后函数的解析式.
解答:解:(1)∵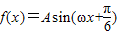 的图象与x轴相邻两个交点之间的距离为
的图象与x轴相邻两个交点之间的距离为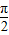 ,
,
∴T=π
又∵ω>0
∴ω=2
又∵图象上一个点为 .
.
∴-2=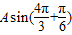
解得A=2
∴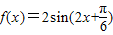
(2)∵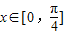
∴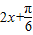 ∈[
∈[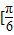 ,
,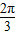 ]
]
当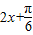 =
=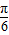 ,即x=0时,f(x)取最小值1
,即x=0时,f(x)取最小值1
当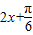 =
=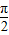 ,即x=
,即x=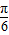 时,f(x)取最大值2
时,f(x)取最大值2
故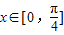 时,函数f(x)的值域为[1,2]
时,函数f(x)的值域为[1,2]
(3)∵将函数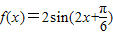 的图象向左平移
的图象向左平移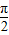 个单位
个单位
可得函数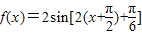 =-
=-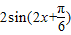 的图象
的图象
再将图象上各点的横坐标变为原来的2倍,纵坐标不变,
可得函数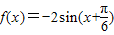 的图象
的图象
点评:本题考查的知识点是正弦型函数解析式是求法,正弦型函数的图象和性质,正弦型函数的图象变换,是正弦型函数图象和性质的综合应用,难度中等.
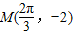 可得A值,进而求出f(x)的解析式;
可得A值,进而求出f(x)的解析式;(2)由
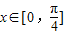 可求出相位角的取值范围,结合正弦函数的性质可得此时函数f(x)的值域;
可求出相位角的取值范围,结合正弦函数的性质可得此时函数f(x)的值域;(3)根据(1)中函数的解析式,结合函数图象的平移变换法则及伸缩变换法则,可得变换后函数的解析式.
解答:解:(1)∵
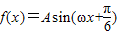 的图象与x轴相邻两个交点之间的距离为
的图象与x轴相邻两个交点之间的距离为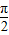 ,
,∴T=π
又∵ω>0
∴ω=2
又∵图象上一个点为
 .
.∴-2=
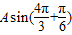
解得A=2
∴
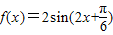
(2)∵
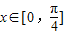
∴
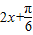 ∈[
∈[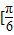 ,
,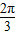 ]
]当
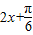 =
=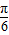 ,即x=0时,f(x)取最小值1
,即x=0时,f(x)取最小值1当
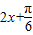 =
=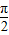 ,即x=
,即x=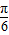 时,f(x)取最大值2
时,f(x)取最大值2故
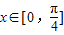 时,函数f(x)的值域为[1,2]
时,函数f(x)的值域为[1,2](3)∵将函数
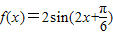 的图象向左平移
的图象向左平移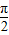 个单位
个单位可得函数
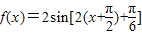 =-
=-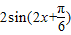 的图象
的图象再将图象上各点的横坐标变为原来的2倍,纵坐标不变,
可得函数
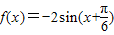 的图象
的图象点评:本题考查的知识点是正弦型函数解析式是求法,正弦型函数的图象和性质,正弦型函数的图象变换,是正弦型函数图象和性质的综合应用,难度中等.

练习册系列答案
相关题目
 (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
. 恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围. ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象