题目内容
直线l绕它与x轴的交点顺时针旋转 ,得到直线
,得到直线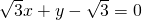 ,则直线l的直线方程
,则直线l的直线方程
- A.
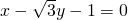
- B.
 x-y-3=0
x-y-3=0 - C.
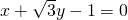
- D.
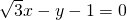
B
分析:先得到直线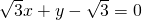 倾斜角θ,由题意可得所求直线的倾斜角等于θ-
倾斜角θ,由题意可得所求直线的倾斜角等于θ- ,可得所求直线的斜率,用点斜式求的直线方程.
,可得所求直线的斜率,用点斜式求的直线方程.
解答:直线直线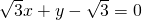 的斜率等于-
的斜率等于- ,设倾斜角等于θ,即θ=
,设倾斜角等于θ,即θ= ,
,
绕它与x轴的交点( ,0)顺时针旋转
,0)顺时针旋转 ,
,
所得到的直线的倾斜角等于θ- ,故所求直线的斜率为tan(
,故所求直线的斜率为tan( -
- ,)=
,)= ,
,
故所求的直线方程为 y-0= (x-
(x- ),即
),即  x-y-3=0,
x-y-3=0,
故选B.
点评:本题考查直线的倾斜角和斜率的关系,以及用点斜式求直线方程的方法,求出所求直线的斜率是解题的关键.
分析:先得到直线
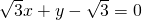 倾斜角θ,由题意可得所求直线的倾斜角等于θ-
倾斜角θ,由题意可得所求直线的倾斜角等于θ- ,可得所求直线的斜率,用点斜式求的直线方程.
,可得所求直线的斜率,用点斜式求的直线方程.解答:直线直线
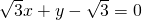 的斜率等于-
的斜率等于- ,设倾斜角等于θ,即θ=
,设倾斜角等于θ,即θ= ,
,绕它与x轴的交点(
 ,0)顺时针旋转
,0)顺时针旋转 ,
,所得到的直线的倾斜角等于θ-
 ,故所求直线的斜率为tan(
,故所求直线的斜率为tan( -
- ,)=
,)= ,
,故所求的直线方程为 y-0=
 (x-
(x- ),即
),即  x-y-3=0,
x-y-3=0,故选B.
点评:本题考查直线的倾斜角和斜率的关系,以及用点斜式求直线方程的方法,求出所求直线的斜率是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目