题目内容
【题目】已知函数![]() .
.
(1)若![]() 是偶函数,求
是偶函数,求![]() 的值;
的值;
(2)设函数![]() ,当
,当![]() 时,
时,![]() 有且只有一个实数根,求
有且只有一个实数根,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)根据![]() 是偶函数,可得
是偶函数,可得![]() ,利用恒等,即可求出结果;
,利用恒等,即可求出结果;
(2)当![]() 时,
时,![]() 有且只有一实根,可得
有且只有一实根,可得![]() ,然后再利用换元法,设
,然后再利用换元法,设![]() ,
,![]() ,转化为
,转化为![]() ,
,![]() 有一实根,根据根的分布,即可求出结果;
有一实根,根据根的分布,即可求出结果;
(3)设![]() ,对分段函数的零点分析可得
,对分段函数的零点分析可得![]() ,即
,即![]() ,
,![]() ,消除
,消除![]() ,整理可得
,整理可得![]() ,进而可得
,进而可得![]() ,据此即可求证结果.
,据此即可求证结果.
(1)![]() 是偶函数,所以
是偶函数,所以![]() ,则
,则![]() .
.
所以![]() .
.
(2)当![]() 时,
时,![]() 有且只有一实根,即
有且只有一实根,即![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,![]() 有一实根,
有一实根,
∵![]() 恒成立,两根之积小于0,所以
恒成立,两根之积小于0,所以 ,
,
∴![]() .
.
(3)不妨设![]() ,则
,则 ,
,
若![]() ,与
,与![]() 矛盾,
矛盾,
若![]() ,与
,与![]() 是单调函数矛盾,
是单调函数矛盾,
所以![]() ;
;
所以![]() ①,
①,![]() ②,
②,
由①,得:![]() ,由②,得:
,由②,得:![]() ;
;
联立①、②消去![]() 得:
得:![]() ,即
,即![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() .
.

练习册系列答案
相关题目
【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐,下表是西南地区某大学近五年的录取平均分高于省一本线分值对比表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
录取平均分高于省一本线分值 | 28 | 34 | 41 | 47 | 50 |
(1)根据上表数据可知,![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)假设2020年该省一本线为520分,利用(1)中求出的回归方程预测2020年该大学录取平均分.
参考公式: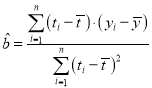 ,
,![]()