题目内容

现有下列命题：

①设a，b为正实数，若a2﹣b2=1，则a﹣b＜1；

②设，均为单位向量，若；

③数列；

④设函数，则关于x的方程f2（x）+2f（x）=0有4个解．

其中的真命题有　　．（写出所有真命题的编号）．

【答案】①②③

【解析】①若a2﹣b2=1，则a2﹣1=b2，

即（a+1）（a﹣1）=b2，

∵a+1＞a﹣1，

∴a﹣1＜b，即a﹣b＜1，①正确；

②若，则，

即2+2cosθ＞1，cosθ＞﹣，

又∵θ∈[0，π]，

∴θ∈[0，），②正确；

③由an=n（n+4）（）n，

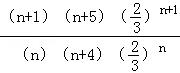令==≥1，

则2（n+1）（n+5）≥3n（n+4），

即n2≤10，所以n＜4，

即n＜4时，an+1＞an，

当n≥4时，an+1＜an，

所以a4最大，故③正确；

令f2（x）+2f（x）=0，

则f（x）=0，或f（x）=﹣2，

∵，

∴当f（x）=0时，

x=1，或x=0，或x=2，

当f（x）=﹣2时，x=10.1或x=0.99，

故方程有5个解，故④错误

故答案为：①②③

练习册系列答案
相关题目
设V是已知平面M上所有向量的集合，对于映射f：V→V，a∈V，记a的象为f（a）．若映射f：V→V满足：对所有a、b∈V及任意实数λ，μ都有f（λa+μb）=λf（a）+μf（b），则f称为平面M上的线性变换．现有下列命题：
①设f是平面M上的线性变换，a、b∈V，则f（a+b）=f（a）+f（b）；
②若e是平面M上的单位向量，对a∈V，设f（a）=a+e，则f是平面M上的线性变换；
③对a∈V，设f（a）=-a，则f是平面M上的线性变换；
④设f是平面M上的线性变换，a∈V，则对任意实数k均有f（ka）=kf（a）．
其中的真命题是
 
（写出所有真命题的编号）
设V是已知平面M上所有向量的集合，对于映射f：V→V，
a
∈V，记
a
的象为f(
a
)．若映射f：V→V满足：对所有
a
，
b
∈V及任意实数λ，μ都有f(λ
a
+μ
b
)=λf(
a
)+μf(
b
)，则f称为平面M上的线性变换．现有下列命题：
①设f是平面M上的线性变换，则f(
0
)=
0

②对
a
∈V设f(
a
)=2
a
，则f是平面M上的线性变换；
③若
e
是平面M上的单位向量，对
a
∈V设f(
a
)=
a
-
e
，则f是平面M上的线性变换；
④设f是平面M上的线性变换，
a
，
b
∈V，若
a
，
b
共线，则f(
a
)，f(
b
)也共线．
其中真命题是
 
（写出所有真命题的序号）
现有下列命题：
①设a，b为正实数，若a2-b2=1，则a-b＜1；
②已知a＞2b＞0，则a2+
8
b(a-2b)
的最小值为16；
③数列{n(n+4)(
2
3
)n}中的最大项是第4项；
④设函数f(x)=
lg|x-1|，x≠1
0，x=1
，则关于x的方程f2（x）+2f（x）=0有4个解．
⑤若sinx+siny=
1
3
，则siny-cos2x的最大值是
4
3
．
其中的真命题有
①②③
①②③
．（写出所有真命题的编号）
现有下列命题：
①设a，b为正实数，若a2-b2=1，则a-b＜1；
②设
a
，
b
均为单位向量，若|
a
+
b
|＞1则θ∈[0，
2π
3
)；
③数列{n(n+4)(
2
3
)n}中的最大项是第4项；
④设函数f(x)=
lg|x-1|，x≠1
0，x=1
，则关于x的方程f2（x）+2f（x）=0有4个解．
其中的真命题有
①②③
①②③
．（写出所有真命题的编号）．
（2012•四川）记[x]为不超过实数x的最大整数，例如，[2]=2，[1.5]=1，[-0.3]=-1．设a为正整数，数列{xn}满足x1=a，xn+1=[
xn+[
a
xn
]
2
](n∈N*)，现有下列命题：
①当a=5时，数列{xn}的前3项依次为5，3，2；
②对数列{xn}都存在正整数k，当n≥k时总有xn=xk；
③当n≥1时，xn＞
a
-1；
④对某个正整数k，若xk+1≥xk，则xk=[
a
]．
其中的真命题有
①③④
①③④
．（写出所有真命题的编号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网