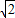题目内容
若 ,
, ,
, 均为单位向量,且
均为单位向量,且 •
• =-
=- ,
, =x
=x +y
+y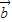 (x,y∈R),则x+y的最大值是( )
(x,y∈R),则x+y的最大值是( )A.2
B.

C.
D.1
【答案】分析:由题设知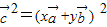 =
=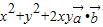 =x2+y2-xy=1,设x+y=t,y=t-x,得3x2-3tx+t2-1=0,由方程3x2-3tx+t2-1=0有解,知△=9t2-12(t2-1)≥0,由此能求出x+y的最大值.
=x2+y2-xy=1,设x+y=t,y=t-x,得3x2-3tx+t2-1=0,由方程3x2-3tx+t2-1=0有解,知△=9t2-12(t2-1)≥0,由此能求出x+y的最大值.
解答:解:∵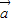 ,
,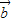 ,
, 均为单位向量,
均为单位向量,
且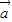 •
•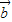 =-
=- ,
,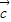 =x
=x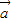 +y
+y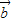 (x,y∈R),
(x,y∈R),
∴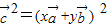 =
=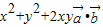 =x2+y2-xy=1,
=x2+y2-xy=1,
设x+y=t,y=t-x,得:x2+(t-x)2-x(t-x)-1=0,
∴3x2-3tx+t2-1=0,
∵方程3x2-3tx+t2-1=0有解,
∴△=9t2-12(t2-1)≥0,
-3t2+12≥0,
∴-2≤t≤2
∴x+y的最大值为2.
故选A.
点评:本题考查平面向量的综合运用,解题时要认真审题,仔细解答,注意平面向量的数量积和换元法的灵活运用.本题也可用基本不等式解答
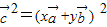 =
=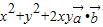 =x2+y2-xy=1,设x+y=t,y=t-x,得3x2-3tx+t2-1=0,由方程3x2-3tx+t2-1=0有解,知△=9t2-12(t2-1)≥0,由此能求出x+y的最大值.
=x2+y2-xy=1,设x+y=t,y=t-x,得3x2-3tx+t2-1=0,由方程3x2-3tx+t2-1=0有解,知△=9t2-12(t2-1)≥0,由此能求出x+y的最大值.解答:解:∵
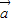 ,
,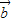 ,
, 均为单位向量,
均为单位向量,且
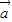 •
•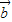 =-
=- ,
,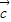 =x
=x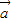 +y
+y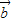 (x,y∈R),
(x,y∈R),∴
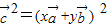 =
=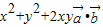 =x2+y2-xy=1,
=x2+y2-xy=1,设x+y=t,y=t-x,得:x2+(t-x)2-x(t-x)-1=0,
∴3x2-3tx+t2-1=0,
∵方程3x2-3tx+t2-1=0有解,
∴△=9t2-12(t2-1)≥0,
-3t2+12≥0,
∴-2≤t≤2
∴x+y的最大值为2.
故选A.
点评:本题考查平面向量的综合运用,解题时要认真审题,仔细解答,注意平面向量的数量积和换元法的灵活运用.本题也可用基本不等式解答

练习册系列答案
相关题目
 ,
, ,
,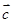 均为单位向量,且
均为单位向量,且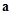 ,
, ,
, 均为单位向量,且
均为单位向量,且 ,
, ,则
,则 的最大值为(
)
的最大值为(
) B . 1 C .
B . 1 C . D.2
D.2 ,
, ,
, 均为单位向量,且
均为单位向量,且 ,
, ,则
,则 的最大值为( )
的最大值为( )

 ,
, ,
, 均为单位向量,且
均为单位向量,且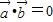 ,
, ,则
,则 的最大值为( )
的最大值为( )