题目内容
在面积为S的△ABC内任取一点P,则△PAB的面积大于
的概率为______.
| S |
| 2 |
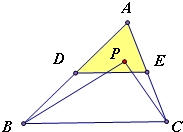
分别取AB、AC中点D、E,连接DE
∵DE是△ABC的中位线,
∴DE上一点到BC的距离等于A到BC距离的一半
设A到BC的距离为h,则当动点P位于线段DE上时,
△PAB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因此,当点P位于△ABC内部,且位于线段DE上方时,△PAB的面积大于
| S |
| 2 |
∵△ADE∽△ABC,且相似比
| DE |
| BC |
| 1 |
| 2 |
∴S△ADE:S△ABC=
| 1 |
| 4 |
由此可得△PAB的面积大于
| S |
| 2 |
| S△ADE |
| S△ABC |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
