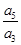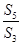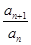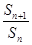题目内容
已知正项等比数列{an}满足:a3=a2+2a1,若存在两项am,an使得 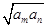 =4a1,则
=4a1,则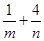 的最小值为 ( ).
的最小值为 ( ).
A.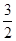 | B. | C.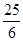 | D.不存在 |
A
解析

练习册系列答案
相关题目
设等比数列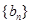 的前
的前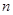 项和为
项和为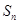 ,若
,若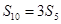 ,则
,则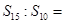 ( )
( )
A.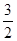 | B.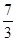 | C.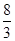 | D.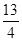 |
已知各项均为正数的等比数列{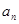 }中,
}中,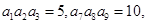 则
则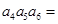 ( )
( )
A.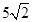 | B.7 | C.6 | D.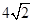 |
已知各项均为正数的等比数列 ,
,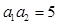 ,
, ,则
,则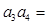 ( )
( )
A.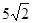 | B.7 | C.6 | D.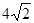 |
设Sn为等比数列{an}的前n项和,8a2+a5=0,则 等于( )
等于( )
| A.-11 | B.-8 | C.5 | D.11 |
设首项为1,公比为 的等比数列{an}的前n项和为Sn,则 ( ).
的等比数列{an}的前n项和为Sn,则 ( ).
| A.Sn=2an-1 | B.Sn=3an-2 |
| C.Sn=4-3an | D.Sn=3-2an |
数列{1+2n-1}的前n项和为( ).
| A.1+2n | B.2+2n | C.n+2n-1 | D.n+2+2n |
等比数列{an}的前n项和公式Sn,若2S4=S5+S6,则数列{an}的公比q的值为 ( ).
| A.-2或1 | B.-1或 2 | C.-2 | D.1 |