题目内容
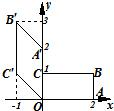如图矩形OABC在变换T的作用下变成了平行四边形OA′B′C′，求变换T所对应的矩阵M．
分析：本题可看成是进行两次变换，第一次旋转变换：由矩形OABC变换成平行四边形OA'B'C'可以看成先将矩形OABC绕着O点旋转90°得到矩形OA''B''C''即M=
=
，第二次切边变换：将矩形OA''B''C''作切变变换得到平行四边形OA'B'C'即N=
，故最终的即为MN
|
|
|
解答：解：由矩形OABC变换成平行四边形OA'B'C'可以看成先将矩形OABC绕着O点旋转90°，
得到矩形OA''B''C''，然后再将矩形OA''B''C''作切变变换得到平行四边形OA'B'C'．
故旋转变换矩阵为：M=
=
切变变换：
→
=
=
∴切变变换矩阵为N=
∴矩阵MN=
=
得到矩形OA''B''C''，然后再将矩形OA''B''C''作切变变换得到平行四边形OA'B'C'．
故旋转变换矩阵为：M=
|
|
切变变换：
|
|
|
|
|
∴切变变换矩阵为N=
|
∴矩阵MN=
|
|
|
点评：本题考查了矩阵变换的性质，矩阵的乘法，属于基础题．
练习册系列答案
相关题目
＝－
＋
交折线OAB于点E．
