题目内容
4．已知函数$f（x）=\left\{\begin{array}{l}{2^{-x}}+1，x≤0\\{log_3}x+ax，x＞0\end{array}\right.$，若f（f（-1））＞4a，则实数a的取值范围是（ ）| A． | （-∞，1） | B． | （-∞，0） | C． | $（-∞，-\frac{1}{5}）$ | D． | （1，+∞） |
分析 根据分段函数值的求法，先求出f（-1）=3，再求f（3）=1+3a，得到关于a的不等式解得即可．
解答 解：f（-1）=21+1=3，
f（3）=log33+3a=1+3a，
∴f（f（-1））=1+3a，
∴1+3a＞4a，
解得a＜1，
故选：A．
点评 本题考查了分段函数的函数值的求法，和不等式的解法，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
15．一个算法程序框图如图所示，其输出结果为（ ）
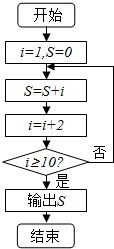
| A． | 9 | B． | 25 | C． | 36 | D． | 49 |
19．已知⊙O1与⊙O2的半径分别为R、r，且它们是方程x2-9x+14=0的两根，若⊙O1与⊙O2相切，则圆心距O1O2等于（ ）
| A． | 5 | B． | 9 | C． | 5或9 | D． | 10或18 |
9．双曲线C；$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0））的左右焦点分别为F1，F2，双曲线C上一点P到右焦点F2的距离是实轴两端点到右焦点距离的等差中项，若△PF1F2为锐角三角形，则双曲线C的离心率的取值范围是（ ）
| A． | （$\frac{1+\sqrt{5}}{2}$，+∞） | B． | （1，1+$\sqrt{3}$） | C． | （$\frac{1+\sqrt{5}}{2}$，1+$\sqrt{3}$） | D． | （$\frac{1+\sqrt{5}}{2}$，2）∪（2，1+$\sqrt{3}$） |
如图，点F是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点，过点F的直线的斜率为3，与双曲线交于P，Q两点，分别过P、Q向右准线作垂线，垂足分别为M，N，且$\overrightarrow{PM}$=3$\overrightarrow{QN}$，求双曲线的离心率的大小．