题目内容
(2013•湖北)已知a为常数,函数f(x)=x(lnx﹣ax)有两个极值点x1,x2(x1<x2)( )
A. |
B. |
C. |
D. |
D
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数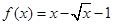 ,
,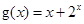 ,
,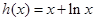 的零点分别为
的零点分别为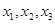 ,则( )
,则( )
A.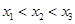 | B.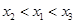 | C.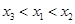 | D.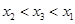 |
已知函数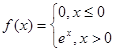 ,则使函数
,则使函数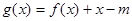 有零点的实数
有零点的实数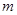 的取值范围是( )
的取值范围是( )
A.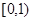 | B. | C. | D.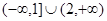 |
已知函数f(x)=sin x- x(x∈[0,π]),那么下列结论正确的是( )
x(x∈[0,π]),那么下列结论正确的是( )
A.f(x)在 上是增函数 上是增函数 |
B.f(x)在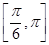 上是减函数 上是减函数 |
C.?x∈[0,π],f(x)>f( ) ) |
D.?x∈[0,π],f(x)≤f( ) ) |
若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)-f(4)=( )
| A.-1 | B.1 | C.-2 | D.2 |
(2013•浙江)已知a、b、c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1),则( )
| A.a>0,4a+b=0 | B.a<0,4a+b=0 |
| C.a>0,2a+b=0 | D.a<0,2a+b=0 |
函数 的值域是( )
的值域是( )
| A.(0,+∞) | B.[1,+∞) |
| C.(0,1] | D.(0,1) |
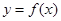 在区间
在区间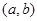 上的导函数为
上的导函数为 ,
,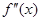 ,若在区间
,若在区间 恒成立,则称函数
恒成立,则称函数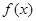 在区间
在区间 ,若对任意的实数
,若对任意的实数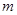 满足
满足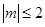 时,函数
时,函数 的最大值为( )
的最大值为( ) 时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )
时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )