题目内容
3.已知数列{an}满足递推式an=2an-1+1(n≥2),其中a4=15(1)求数列{an}的通项公式;
(2)已知数列{bn},有bn=$\frac{n}{{a}_{n}+1}$,求数列{bn}的前n项和Sn.
分析 (1)通过对an=2an-1+1(n≥2)变形可知an+1=2(an-1+1)(n≥2),利用a4+1=16可知an+1=2n,进而可得结论;
(2)通过(1)知bn=$\frac{n}{{2}^{n}}$,利用错位相减法计算即得结论.
解答 解:(1)∵an=2an-1+1(n≥2),
∴an+1=2(an-1+1)(n≥2),
即数列{an+1}是公比为2的等比数列,
又∵a4+1=15+1=16,
∴an+1=16•2n-4=2n,
∴an=-1+2n;
(2)由(1)知bn=$\frac{n}{{a}_{n}+1}$=$\frac{n}{{2}^{n}}$,
∴Sn=$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+…+n•$\frac{1}{{2}^{n}}$,①
$\frac{1}{2}$Sn=$\frac{1}{{2}^{2}}$+2•$\frac{1}{{2}^{3}}$+…+(n-1)•$\frac{1}{{2}^{n}}$+n•$\frac{1}{{2}^{n+1}}$,②
①-②得:$\frac{1}{2}$Sn=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$-n•$\frac{1}{{2}^{n+1}}$
=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$
=1-$\frac{n+2}{{2}^{n+1}}$,
整理得:Sn=2-$\frac{n+2}{{2}^{n}}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.

| A. | ($\frac{π}{2}$,$\frac{3π}{4}$)∪(π,$\frac{5π}{4}$) | B. | ($\frac{π}{4},\frac{π}{2}$)∪(π,$\frac{5π}{4}$) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$)∪($\frac{5π}{4},\frac{3π}{2}$) | D. | ($\frac{π}{4},\frac{π}{2}$)∪($\frac{3π}{4},π$) |
 如图,△OAB是边长为4的等边三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t),试求函数f(t)的解析式.
如图,△OAB是边长为4的等边三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t),试求函数f(t)的解析式.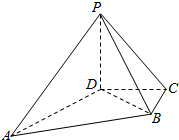 如图,在四棱锥P-ABCD中,PD=4,DC=DB=3,PB=PC=5,AD⊥DB.
如图,在四棱锥P-ABCD中,PD=4,DC=DB=3,PB=PC=5,AD⊥DB.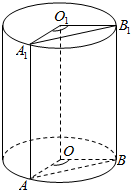 如图所示,过圆柱的两条母线AA1和BB1的截面A1 ABB1 的面积为S,母线AA1 的长为l,∠A1 O1 B1=90°,求此圆柱的体积.
如图所示,过圆柱的两条母线AA1和BB1的截面A1 ABB1 的面积为S,母线AA1 的长为l,∠A1 O1 B1=90°,求此圆柱的体积.