题目内容
(本小题共12分)已知f(x)=m(x-2m)(x+m+3),g(x)= -2,若同时满足条件:
-2,若同时满足条件:
① x∈R,f(x) <0或g(x) <0;②
x∈R,f(x) <0或g(x) <0;② x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
x∈(﹣∝, ﹣4),f(x)g(x) <0。求m的取值范围。
【答案】
(一)此满足条件①的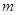 的取值范围为
的取值范围为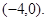
(二)综上所述满足①②两个条件的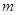 的取值范围为
的取值范围为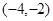
【解析】
试题分析:根据已知题意得到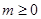 时不能保证对
时不能保证对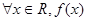 <0或
<0或 <0成立.
<0成立.
那么只有m<0时,则根据二次函数图像与指数函数图像的位置关系,在满足前提条件下的,可知参数m的范围。
解:(一)由题意可知,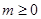 时不能保证对
时不能保证对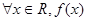 <0或
<0或 <0成立.
<0成立.
⑴当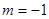 时,
时,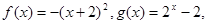 此时显然满足条件①;
此时显然满足条件①;
⑵当-1<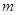 <0时,
<0时,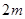 >
>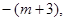 要使其满足条件①,则需-1<
要使其满足条件①,则需-1<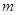 <0且
<0且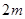 <1,解得-1<
<1,解得-1<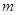 <0;
<0;
⑶当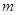 <-1时,
<-1时,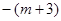 >
>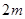 ,要使其满足条件①,则需
,要使其满足条件①,则需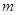 <-1且
<-1且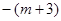 <1,
<1,
解得-4<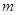 <-1. 因此满足条件①的
<-1. 因此满足条件①的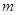 的取值范围为
的取值范围为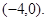
(二)在满足条件①的前提下,再探讨满足条件②的取值范围。
⑴当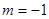 时,在
时,在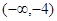 上,
上,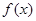 与
与 均小于0,不合题意;
均小于0,不合题意;
⑵当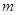 <-1时,则需
<-1时,则需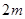 <-4,即
<-4,即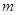 <-2,所以-4<
<-2,所以-4<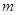 <-2.
<-2.
⑶当-1<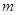 <0时,则需
<0时,则需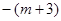 <-4,即
<-4,即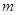 >1,此时无解。
>1,此时无解。
综上所述满足①②两个条件的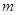 的取值范围为
的取值范围为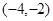
考点:本题主要是考查二次函数图像与指数函数图像的运用。
点评:解决该试题的关键是理解两个条件,翻译为图像中的二次函数中的两个根 的位置,以及对于m的分类讨论思想的运用。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间; 上任意一点P到两个定点F1(-
上任意一点P到两个定点F1(- ,0)和F2(
,0)和F2( 与曲线
与曲线 为坐标原点),求直线
为坐标原点),求直线
 的最小正周期和最小值;
的最小正周期和最小值; ,
, ,求证:
,求证: .
.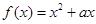 的最小值不小于
的最小值不小于 , 且
, 且 .
. 的解析式;
的解析式; 的最小值为实数
的最小值为实数 的函数
的函数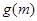 ,求函数
,求函数 ,集合
,集合
 ,求实数
,求实数 的取值范围.
的取值范围.