��Ŀ����
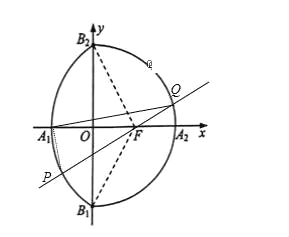
����Ŀ���Ѱ���Բ![]() ��x��0����Բ����x��c��2+y2=a2��x��0���ϳɵ����߳�������Բ��������F��c��0��Ϊ����Բ���ҽ��㣮��ͼ��A1��A2��B1��B2�ֱ�������Բ����x�ᡢy��Ľ��㣬��֪��B1FB2=
��x��0����Բ����x��c��2+y2=a2��x��0���ϳɵ����߳�������Բ��������F��c��0��Ϊ����Բ���ҽ��㣮��ͼ��A1��A2��B1��B2�ֱ�������Բ����x�ᡢy��Ľ��㣬��֪��B1FB2=![]() ������FB1A1B2�����Ϊ
������FB1A1B2�����Ϊ![]() ��
��
��1����a��c��ֵ��
��2������F����б��Ϊ����ֱ�߽�����Բ����P��Q���㣬�Խ���A1PQ���ܳ�L��ʾΪ���ĺ�����
��3���ڣ�2���������£�����A1PQ���ܳ�Lȡ�����ֵʱ����̽����A1PQ������Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ�����������ȡֵ��Χ��
-��
���𰸡���1��a=2��c=1����2������������3��![]() .
.
��������
��1��������Բ��������![]() ���������������ʽ������з��̿����
���������������ʽ������з��̿����![]() ��ֵ.����
��ֵ.����![]() �����
�����![]() ��ֵ��2���ɣ�1���Ľ��������Բ�ķ��̺�Բ�ķ���.��
��ֵ��2���ɣ�1���Ľ��������Բ�ķ��̺�Բ�ķ���.��![]() �ֳ�
�ֳ�![]() ���࣬������Բ�Ķ���ͽ�������������������
���࣬������Բ�Ķ���ͽ�������������������![]() ���ܳ�.��3���ɣ�2���ķ�����֪��������
���ܳ�.��3���ɣ�2���ķ�����֪��������![]() ���ȡ�����ֵʱ��
���ȡ�����ֵʱ��![]() �ڰ���Բ��.�����ҳ���ʽ���
�ڰ���Բ��.�����ҳ���ʽ���![]() �ij������õ㵽ֱ�ߵľ��빫ʽ���
�ij������õ㵽ֱ�ߵľ��빫ʽ���![]() ��
��![]() �ľ��룬�г�������
�ľ��룬�г�������![]() ����ı���ʽ�����û�Ԫ����������ȡֵ��Χ.
����ı���ʽ�����û�Ԫ����������ȡֵ��Χ.
��1��������Բ��������![]() ���������������ʽ��
���������������ʽ��![]() ������
������![]() ����
����![]() .
.
��2���ɣ�1��֪![]() ���ʰ���Բ����Ϊ
���ʰ���Բ����Ϊ![]() ��Բ���ķ���Ϊ
��Բ���ķ���Ϊ![]() .��
.��![]() ǡ������Բ����.��Ȼֱ��
ǡ������Բ����.��Ȼֱ��![]() ��б�ʲ���Ϊ
��б�ʲ���Ϊ![]() ������
������![]() �ķ���Ϊ
�ķ���Ϊ![]() .�ٵ�
.�ٵ�![]() ʱ��
ʱ��![]() �ֱ���Բ���Ͱ���Բ�ϣ�
�ֱ���Բ���Ͱ���Բ�ϣ�![]() Ϊ��Ϊ
Ϊ��Ϊ![]() �ĵ��������Σ�
�ĵ��������Σ�![]() ����
����![]() ���ܳ�
���ܳ�![]()
�ڵ�![]() ʱ��
ʱ��![]() �ֱ�Բ���Ͱ���Բ�ϣ�ͬ���ٿ����
�ֱ�Բ���Ͱ���Բ�ϣ�ͬ���ٿ����![]() ���ܳ�
���ܳ�![]() .
.
�۵�![]() ʱ��
ʱ��![]() ���ڰ���Բ�ϣ���ʱ
���ڰ���Բ�ϣ���ʱ![]() ���ܳ�
���ܳ�![]() .
.
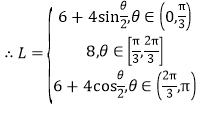
��3���ɣ�2��֪����![]() ���ڰ���Բ��ʱ��
���ڰ���Բ��ʱ��![]() ���ܳ�ȡ�����ֵ.��ֱ��
���ܳ�ȡ�����ֵ.��ֱ��![]() �ķ��̴�����Բ���̲������
�ķ��̴�����Բ���̲������![]() ������
������![]() �����ҳ���ʽ��
�����ҳ���ʽ��![]() ����
����![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() ����������
����������![]() �����
�����![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ϵ�������
�ϵ�������![]() ������
������![]() .
.